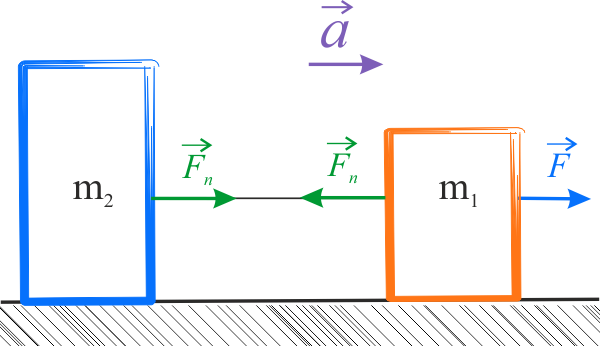
Zadanie 3.4.2.1
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa pierwszego ciała \(m_1=1\,\mathrm{kg}\),
- masa drugiego ciała \(m_2=2\,\mathrm{kg}\),
- maksymalna wartość naprężenia \(F_{Nmax}=20\,\mathrm{N}\).
Szukane:
- maksymalna wartość siły niepowodująca zerwania nici \(F\).
Odpowiedź
Maksymalna siła pozioma, jaką można przyłożyć do pierwszego z tych ciał, aby nić się nie zerwała, wynosi \(F=30\,\mathrm{N}\).
Polecenie
Poniżej przedstawione są dwa stwierdzenia. Wybierz jedno prawidłowe.
Wybór 1 z 2
W poziomie, na ciało pierwsze, działa tylko siła naciągu nici łączącej oba klocki, natomiast na ciało drugie działa siła zewnętrzna.
Wybór 2 z 2
W poziomie, na ciało pierwsze, działa siła zewnętrzna oraz przeciwna do niej siła naciągu nici łączącej oba klocki, natomiast na ciało drugie tylko siła naciągu nici.
Polecenie
Oblicz maksymalną siłę poziomą, jaką można przyłożyć do pierwszego z tych ciał, aby nić się nie zerwała. Wybierz jedną prawidłową odpowiedź wśród czterech, przedstawionych poniżej.
\(F=10\,\mathrm{N}\)
\(F=20\,\mathrm{N}\)
Rozwiązanie
Klocki leżą na doskonale gładkim stole, więc w rozważaniach pomijamy siłę tarcia.
Na klocek pierwszy działają dwie siły:
Na klocek drugi działa tylko jedna siła
Z drugiego równania otrzymujemy \(\displaystyle{a=\frac{F_n}{m_2}}\). Wartość tą podstawiamy do równania pierwszego:
W ten sposób otrzymaliśmy bezpośredni związek między siłą przyłożoną do ciała pierwszego a naprężeniem nici. Ponieważ nić może wytrzymać naprężenie nie przekraczające \(20\,\mathrm{N}\), to maksymalna siła, jaką można przyłożyć siłę do pierwszego ciała, wynosi:
Odpowiedź
Maksymalna siła pozioma, jaką można przyłożyć do pierwszego z tych ciał, aby nić się nie zerwała, wynosi \(F=30\,\mathrm{N}\).