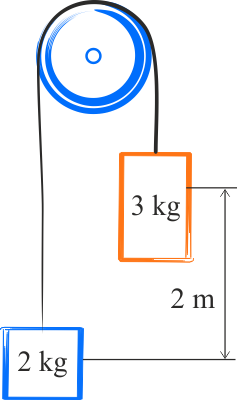
Zadanie 3.4.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa pierwszego ciężarka \(m_1=2\,\mathrm{kg}\),
- masa drugiego ciężarka \(m_2=3\,\mathrm{kg}\),
- różnica wysokości pomiędzy położeniami ciężarków \(d=2\,\mathrm{m}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- naprężenie nici podczas ruchu ciężarków \(F_N\),
- wartość przyspieszenia klocków \(a\),
- czas, po którym ciężarki znajdą się na tej samej wysokości \(t\).
Odpowiedź
Naprężenie nici podczas ruchu ciężarków wynosi \(F_N=24\,\mathrm{N}\), wartość przyspieszenia \(\displaystyle{a=2\,\frac{m}{s^2} }\). Na tej samej wysokości ciężarki znajdą się po \(1\,\mathrm{s}\) ruchu.
Polecenie
Jeśli puścimy klocki swobodnie to klocek cięższy \(m_2\) zacznie opadać w dół, a klocek lżejszy \(m_1\) - w górę. Zastanów się, jakie siły działają na klocki i nić. Zapisz układ równań, który opisuje działające siły w omawianej sytuacji. Wybierz spośród czterech jeden układ, który przypomina Twój wynik.
\(\left\{\begin{matrix} a\,m_1=F_N-m_1\,g\\ a\,m_2=m_2\,g-F_N \end{matrix}\right.\)
\(\left\{\begin{matrix} a\,m_1=F_N+m_1\,g\\ a\,m_2=F_N+m_2\,g \end{matrix}\right.\)
Rozwiązanie
Ponieważ nić jest nierozciągliwa, ciężarki poruszają się z jednakową prędkością i przyspieszeniem. Każdy z ciężarków porusza się pod wpływem następujących sił: siły ciężkości skierowanej w dół oraz siły naprężenia nici skierowanej w górę. Ponieważ nić i bloczek są nieważkie, to wartości sił naprężenia obu końców nici są takie same. Do momentu spotkania każdy z ciężarków przebędzie tę samą drogę \(1\,\mathrm{m}\), będącą połową odległości pomiędzy nimi.
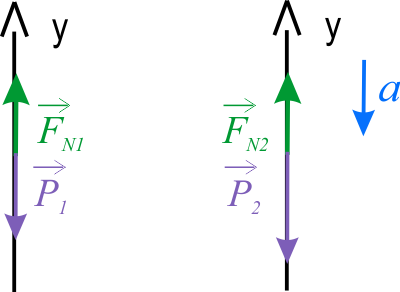
Na rysunku narysowane są siły działające na ciężarki o masach \(m_1\) i \(m_2\). Odpowiednio Są to: siły ciężkości \(P_1\) i \(P_2\) oraz siły naciągu nici \(F_{N1}\) i \(F_{N2}\). Ponieważ nić i bloczek są nieważkie to wartości \(F_{N1}\) i \(F_{N2}\) są takie same - na diagramie sił długości wektorów \(F_{N1}\) i \(F_{N2}\) są jednakowe.
Uwzględniając fakt, że wszystkie siły w układzie działają wzdłuż tych samych, albo równoległych prostych, na poniższym rysunku wektory został zastąpione ich wartościami bezwzględnymi. Uwzględniono, że wartości sił ciężkości wynoszą: \(P_1=m_1\,g\) i \(P_2=m_2\,g\), a wartości sił naprężenia nici są jednakowe – zostały oznaczone \(F_N\).
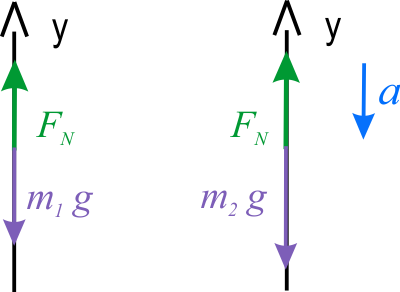
Na podstawie diagramu sił oraz II zasady dynamiki, możemy napisać równania:
Polecenie
Wyznacz wartość przyspieszenia oraz naciągu nici. Wybierz jedną prawidłową odpowiedź, wśród czterech przedstawionych poniżej.
\(\displaystyle{a=0,5\,\mathrm{\frac{m}{s^2}}}\)
\(F_N=6\,\mathrm{N}\)
\(F_N=12\,\mathrm{N}\)
\(F_N=18\,\mathrm{N}\)
\(F_N=24\,\mathrm{N}\)
Rozwiązanie
Przekształcając układ równań
Dodając stronami powyższe równania mamy: \[am_1+am_2=-m_1g+m_2g+F_N-F_N\] \[a(m_1+m_2)=g(m_2-m_1)\]
W celu obliczenia naciągu nici przekształcamy pierwsze równanie układu równań do postaci
Polecenie
Oblicz, po jakim czasie ciężarki znajdą na tej samej wysokości. Wybierz jedną prawidłową odpowiedź, wśród trzech przedstawionych poniżej.
Rozwiązanie
Ruch ciężarków jest ruchem jednostajnie przyspieszonym z prędkością początkową równą zero. Dla tego ruchu równanie wiążące drogę i czas ruchu, którego rozwiązaniem jest szukany czas ruchu ciężarków do momentu ich spotkania, ma postać:
Odpowiedź
Naprężenie nici podczas ruchu ciężarków wynosi \(F_N=24\,\mathrm{N}\), wartość przyspieszenia \(\displaystyle{a=2\,\frac{m}{s^2} }\). Na tej samej wysokości ciężarki znajdą się po \(1\,\mathrm{s}\) ruchu.