Zadanie 3.4.2.3
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa ciężaru \(m\),
- przyspieszenie ziemskie \(g\).
Szukane:
- wartość sił: \(F_A\), \(F_B\) i \(F_C\).
Odpowiedź
Wartości sił wynoszą: \(\displaystyle{F_A=\frac{1}{2}m\,g}\), \(\displaystyle{F_B=\frac{1}{4}m\,g}\), \(\displaystyle{F_C=\frac{1}{8}m\,g}\).
Polecenie
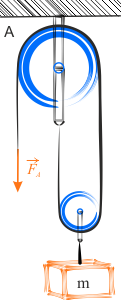
Zastanów się, jakie siły naciągów działają na liny. Wyznacz siłę \(F_A\), jaką należy przyłożyć do oznaczonego miejsca, by zawieszony ciężar pozostał w bezruchu. Wybierz jedną prawidłową wartość siły, spośród czterech przedstawionych poniżej.
\(\displaystyle{F_A=\frac{1}{16}m\,g}\)
\(\displaystyle{F_A=\frac{1}{8}m\,g}\)
Rozwiązanie
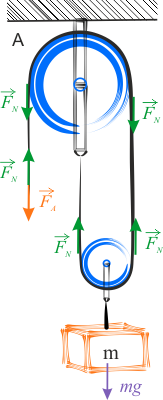
W przykładzie pierwszym występuje jeden bloczek ruchomy i jeden nieruchomy. Bloczek większy jest nieruchomy, ponieważ krążek ten może się tylko obracać, nie zaś poruszać ruchem postępowym.
Rozpatrywane bloczki są idealnie gładkie, więc wszystkie zaznaczone siły naciągu \(F_N\) są takie same. Ciężarek o masie \(m\) jest utrzymywany przez dwie siły naciągu i wiemy, że ma pozostać w bezruchu, więc możemy napisać:
Ten warunek wynika z tego, że aby masa pozostała w spoczynku lub poruszała się jednostajnie to góry, siła naciągu musi równoważyć ciężar. Wykonując proste przekształcenie otrzymujemy:
Jeżeli działamy na linkę siłą \(F_A\), to linka działa na nas siłą \(-F_A\) (III zasada dynamiki). Skoro linka jest naciągnięta siłą \(F_N\) to znaczy, że my także musimy zadziałać taką siłą. Zatem \(F_A=F_N\). Ostatecznie otrzymujemy:
Informacja
Poniżej przedstawiona jest animacja ilustrująca wielkość siły, jaka wymagana jest do podniesienia ciężaru za pomocą omawianego układu bloczków (etap 1) oraz ruch w przypadku podnoszenia ciężaru (etap 2).
W etapie pierwszym animacji umieszczone są szare trójkąty. Klikając w nie zobaczysz, jak zmienia się wartość siły potrzebnej do podtrzymania różnych ciężarów.
Polecenie
Zastanów się, jakie siły naciągów działają na liny. Wyznacz siłę \(F_B\), jaką należy przyłożyć do oznaczonego miejsca, by zawieszony ciężar pozostał w bezruchu. Wybierz jedną prawidłową wartość siły, spośród czterech przedstawionych poniżej.
Rozwiązanie
W przykładzie drugim przedstawiony jest wielokrążek - dwukrążek podwójny. Podobnie jak poprzednio, bloczki są idealnie gładkie, więc wszystkie zaznaczone siły naciągu \(F_N\) są takie same. Ciężarek o masie \(m\) jest utrzymywany przez cztery siły naciągu i wiemy, że ma pozostać w bezruchu, więc możemy napisać:
Ten warunek wynika z tego, że aby masa pozostała w spoczynku lub poruszała się jednostajnie to góry, siła naciągu musi równoważyć ciężar. Wykonując proste przekształcenie otrzymujemy:
Jeżeli działamy na linkę siłą \(F_B\), to linka działa na nas siłą \(-F_B\) (III zasada dynamiki). Skoro linka jest naciągnięta siłą \(F_N\) to znaczy, że my także musimy zadziałać taką siłą. Zatem \(F_B=F_N\). Ostatecznie otrzymujemy:
Informacja
Poniżej przedstawiona jest animacja ilustrująca wielkość siły, jaka wymagana jest do podniesienia ciężaru za pomocą omawianego układu bloczków (etap 1) oraz ruch w przypadku podnoszenia ciężaru (etap 2).
W etapie pierwszym animacji umieszczone są szare trójkąty. Klikając w nie zobaczysz, jak zmienia się wartość siły potrzebnej do podtrzymania różnych ciężarów.
Polecenie
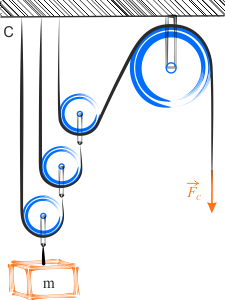
Zastanów się, jakie siły naciągów działają na liny. Wyznacz siłę \(F_C\), jaką należy przyłożyć do oznaczonego miejsca, by zawieszony ciężar pozostał w bezruchu. Wybierz jedną prawidłową wartość siły, spośród czterech przedstawionych poniżej.
Rozwiązanie
W przykładzie ostatnim przedstawiony jest
Jest to układ \(k\) bloczków ruchomych i jednego bloczka nieruchomego. Jeżeli potraktujemy bloczek pierwszy jako podstawę potęgi, to następne bloczki ruchome będą się układać, jak wykładniki potęg tej podstawy. Ma to też związek warunkiem równowagi dla takiego układu. Warunek równowagi dla wielokrążka potęgowego: \[\displaystyle{F=\frac{mg}{2^{k-1}}}\] gdzie \(k\) jest ilością krążków oraz \(k\in N_+\) i \(k>2\).
Podobnie jak poprzednio, bloczki są idealnie gładkie. Każdy bloczek ruchomy wisi na innej linie, co za tym idzie, na każdej linie zaznaczone są inne siły naciągu.
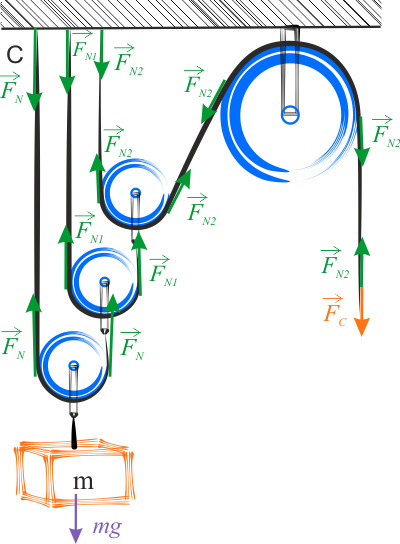
Ciężarek o masie \(m\) jest utrzymywany przez dwie siły naciągu i wiemy, że ma pozostać w bezruchu, więc możemy napisać:
Po prostych przekształceniach otrzymujemy:
Wynika to z tego, że naciąg nici zmniejsza się co każdy bloczek dwa razy.
Jeżeli działamy na linkę siłą \(F_C\), to linka działa na nas siłą \(-F_C\) (III zasada dynamiki). Skoro linka jest naciągnięta siłą \(F_{N2}\) to znaczy, że my także musimy zadziałać taką siłą. Zatem \(F_C=F_{N2}\). Ostatecznie otrzymujemy:
Odpowiedź
Wartości sił wynoszą: \(\displaystyle{F_A=\frac{1}{2}m\,g}\), \(\displaystyle{F_B=\frac{1}{4}m\,g}\), \(\displaystyle{F_C=\frac{1}{8}m\,g}\).