Zadanie 3.4.2.4
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 3. Zasady dynamiki
  3. 3.4. Proste układy mechaniczne
  4. 3.4.2 Trening
  5. Zadanie 3.4.2.4
DOI: 10.37190/OZE-FizykaCw1-r3

 Zadanie 3.4.2.4

Układ bloczków
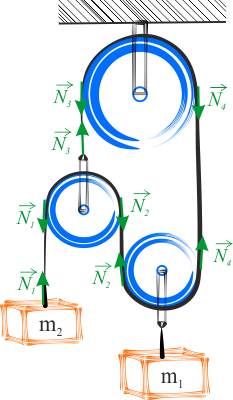
Dwie masy \(m_1\) i \(m_2\) zawieszone są w układzie bloczków przedstawionym na rysunku. Z jakim przyspieszeniem porusza się masa \(m_1\)? Zakładamy, że liny są nieważkie, wiotkie i nierozciągliwe. Bloczki są nieważkie. Fragmenty lin nie znajdujące się na bloczkach pozostają stale proste. Pomiń tarcie i opór powietrza.

 Rysunek

Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa ciała pierwszego \(m_1\),
- masa ciała drugiego \(m_2\),
- przyspieszenie grawitacyjne \(g\).

Szukane:
- przyspieszenie ciała pierwszego \(a_1\).

Odpowiedź

Masa \(m_1\) porusza się z przyspieszeniem \(a_1=g\).

Polecenie

Przyjrzyj się rozkładowi sił zaznaczonych na rysunku. Które z czterech, poniżej przedstawionych, równań są prawidłowe?

Wybór 1 z 4

\(N_1=N_2=N_3=N_4\)

Odpowiedź prawidłowa
Bloczki są idealnie gładkie, więc wszystkie zaznaczone siły naciągu, na danej linie, są takie same.

Wybór 2 z 4

\(N_1=2N_2=3N_3=4N_4\)

Odpowiedź nieprawidłowa
Wartości sił naciągów nie mogą rosnąć, gdy bloczki wiszą na jednej linie i są idealnie gładkie.

Wybór 3 z 4

\(N_1+N_2=N_3\)

Odpowiedź prawidłowa
Z analizy rozkładu sił przy bloczku znajdujacym sie najbliżej lewej strony rysunku.

Wybór 4 z 4

\(N_4=N_1+N_3\)

Odpowiedź nieprawidłowa
Brak zgodności z zasadami dynamiki Newtona.

Polecenie

Przyjrzyj się poprawnym odpowiedzią zaznaczonym powyżej. Co możesz wywnioskować z tych zależności?

Rozwiązanie

Z rozważań dotyczących rozkładu sił, doszliśmy do następujących zależności

\(N_1=N_2=N_3=N_4\) oraz \(N_1+N_2=N_3\).

Oznaczmy, że \(N=N_1=N_2=N_3=N_4\), więc stąd mamy \(N+N=N_3\), czyli \(2N=N_3\).
Kolejno, z dwóch równań otrzymaliśmy, że
\(N_3=N\) oraz \(N_3=2N\).

Sytuacja taka jest możliwa, gdy \(N=0\). Jeżeli \(N_2=N_4=0\), to na bloczek najniżej opuszczony nie działa żadna siła naciągu, więc masa \(m_1\) będzie spadać swobodnie z przyspieszeniem \(a_1=g\).