Zadanie 3.4.2.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.4. Proste układy mechaniczne
  4. 3.4.2 Trening
  5. Zadanie 3.4.2.5

 Zadanie 3.4.2.5

Układ mas z bloczkiem
Na stole umocowano jedną za druga masy \(m_1=60\,\mathrm{kg}\) i \(m_2=40\,\mathrm{kg}\). Współczynniki tarcia kinetycznego występującego pomiędzy stołem a masami, wynoszą odpowiednio \(\mu_1=0,4\) oraz \(\mu_2=0,3\). Te dwa ciała umocowano przy pomocy bloczka z masą \(M=70\,\mathrm{kg}\) - patrz rysunek. Znajdź przyspieszenie układu i naprężenia wszystkich nici.

Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
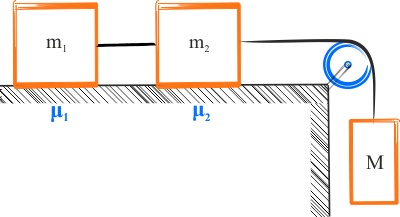
- masa ciała pierwszego \(m_1=60\,\mathrm{kg}\),
- masa ciała drugiego \(m_2=40\,\mathrm{kg}\),
- masa ciała trzeciego \(M=70\,\mathrm{kg}\),
- współczynnik tarcia kinetycznego dla ciała pierwszego wynosi \(\mu_1=0,4\),
- współczynnik tarcia kinetycznego dla ciała drugiegowynosi \(\mu_2=0,3\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- przyspieszenie układu mas \(a\),
- naprężenie nici łączącej masę pierwszą i drugą \(N_1\),
- naprężenie nici łączącej masę drugą oraz masę \(M\): \(N_2\).

Odpowiedź

Przyspieszenie układu mas wynosi \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\), natomiast siły naprężeń nici maja odpowiednio wartości \(N_1=360\,\mathrm{N}\) oraz \(N_2=560\,\mathrm{N}\).

Polecenie

Napisz trzy równania opisujące siły działające na poszczególne masy w kierunku ich ruchu. Wyznacz wartość przyspieszenia układu i wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\displaystyle{a=3\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{a=4\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

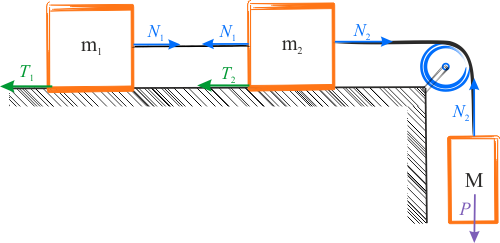
Układ dwóch mas zamocowany jest do ciężaru, który opadając powoduje ich ruch w prawo. Zakładamy, że siły, których zwrot jest zgodny z kierunkiem ruchu, są dodatnie, natomiast pozostałe mają wartość ujemną. Układ równań dla poruszającego się układu mas wygląda następująco:

\(\left\{\begin{matrix} m_1a= &N_1-\mu_1m_1g \\ m_2a= &N_2-N_1-\mu_2m_2g \\ Ma= &Mg-N_2 \end{matrix}\right.\)

Dodając równania stronami otrzymujemy:

\((m_1+m_2+M)a=Mg-\mu_1m_1g-\mu_2m_2g\)

Przyspieszenie układu opisuje wzór

\(\displaystyle{a=\frac{g(M-\mu_1m_1-\mu_2m_2}{m_1+m_2+M}}\)

\(\displaystyle{a=\frac{10\cdot (70-0,4\cdot 60-0,3\cdot 40)}{60+40+70}=2\,\mathrm{\frac{m}{s^2}} }\)

Siły działające na masy w układzie z bloczkiem. Na diagramie siły są reprezentowane przez ich wartości bezwzględne.

Rysunek
Siły działające w układzie mas. Siły, które pozostaja w równowadze i nie powoduja ruchu zostały pominięte (\(R_1\), \(P_1\), \(R_2\), \(P_2\)).

Polecenie

Oblicz siłę naciągu nici łączącej ciało pierwsze z drugim oraz siłę tarcia \(T_2\). Wskaż jedną prawdziwą zależność pomiędzy tymi siłami, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(2T_2=N_1\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(T_2=2N_1\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(3T_2=N_1\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(T_2=3N_1\)

Odpowiedź nieprawidłowa

Rozwiązanie

Do obliczenia siły naciągu nici \(N_1\) posłużymy się pierwszym równaniem z wyprowadzonego wcześniej okładu równań.

\(\left\{\begin{matrix} m_1a= &N_1-\mu_1m_1g \\ m_2a= &N_2-N_1-\mu_2m_2g \\ Ma= &Mg-N_2 \end{matrix}\right.\)

\(\eqalign{N_1 &=m_1a+\mu_1m_1g \\ N_1 &=60\cdot 2+0,4\cdot 60\cdot 10=120+240 \\ N_1 &=360\,\mathrm{N} }\)

Siła tarcia pomiędzy stołem a klockiem drugim wynosi:

\(\eqalign{T_2 &=\mu_2m_2g \\ T_2 &=0,3\cdot 40\cdot 10=120\,\mathrm{N} }\)

Pomiędzy siłą naciągu \(N_1\) a siłą tarcia \(T_2\) zachodzi zależność:

\(\displaystyle{\frac{N_1}{T_2}=\frac{360}{120}=3}\)

\(N_1=3T_2\)

Polecenie

Oblicz drugą siłę naciągu pomiędzy ciałem \(m_2\) i \(M\). Wskaż jedną prawdziwą odpowiedź, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(N_2-N_1=200\,\mathrm{N}\)

Odpowiedź prawidłowa

Wybór 2 z 4

\(N_1+N_2=1000\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4
 
\(N_1=120\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4
 
\(N_2=240\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Do obliczenia siły naciągu nici \(N_2\) posłużymy się trzecim równaniem z wyprowadzonego wcześniej okładu równań.

\(\left\{\begin{matrix} m_1a= &N_1-\mu_1m_1g \\ m_2a= &N_2-N_1-\mu_2m_2g \\ Ma= &Mg-N_2 \end{matrix}\right.\)

\(\eqalign{N_2 &=Mg-Ma=M(g-a) \\ N_2 &=70(10-2)=560 \\ N_2 &=560\,\mathrm{N} }\)

Obliczona wcześniej wartość siły naciągu wynosi \(N_1=360\,\mathrm{N}\), więc prawdziwe jest stwierdzenie, że

\(N_2-N_1=560-360=200\,\mathrm{N}\)

Odpowiedź

Przyspieszenie układu mas wynosi \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\), natomiast siły naprężeń nici maja odpowiednio wartości \(N_1=360\,\mathrm{N}\) oraz \(N_2=560\,\mathrm{N}\).