Zadanie 3.4.2.6
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.4. Proste układy mechaniczne
  4. 3.4.2 Trening
  5. Zadanie 3.4.2.6

 Zadanie 3.4.2.6

Bloczek i równia
Dwa ciała o masach \(m_1=5\,\mathrm{kg}\) oraz \(m_2=12\,\mathrm{kg}\), powiązane nierozciągliwą nicią, umieszczono na równi pochyłej. Wyznacz przyspieszenie ciał oraz naciąg nici. Współczynnik tarcia między masami a podłożem wynosi \(\mu=0,2\), kąty między równią a podłożem wynoszą odpowiednio \(\alpha=30^{\circ}\) oraz \(\beta=45^{\circ}\).

 Rysunek

Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa ciała pierwszego \(m_1=5\,\mathrm{kg}\),
- masa ciała drugiego \(m_2=12\,\mathrm{kg}\),
- współczynnik tarcia między masami a podłożem \(\mu=0,2\),
- kąt między równią a podłożem po stronie masy pierwszej \(\alpha=30^{\circ}\),
- kąt między równią a podłożem po stronie masy drugiej \(\beta=45^{\circ}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- przyspieszenie ciał \(a\),
- siła naciągu nici \(F_N\).

Odpowiedź

Przyspieszenie ciał wynosi \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}} }\), natomiast siła naciągu nici przyjmuje wartość \(F_N=43,7\,\mathrm{N}\).

Polecenie

Oblicz przyspieszenie poruszających się ciał i wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{a=1,6\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(\displaystyle{a=2,6\,\mathrm{\frac{m}{s^2}} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

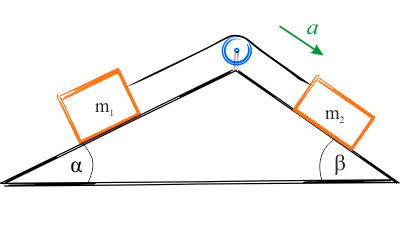
Układ dwóch mas umieszczony jest na równi o dwóch różnych kątach nachylenia. Układ ciał porusza się w kierunku większego kąta nachylenia \(\beta\). Ponieważ sznur jest nierozciągliwy, to obydwa ciała poruszają się z tą samą wartością przyspieszenia, a ponieważ bloczek i sznur są nieważkie (zakładamy, że ich masa jest dużo mniejsza od mas obu ciał), wartości siły naprężenia sznura \(F_N\) z obu jego końców są takie same. Oba ciała poruszają się ruchem przyspieszanym więc zastosujemy II zasadę dynamiki do opisu ich ruchu. Aby znaleźć siłę wzajemnego oddziaływania (poprzez sznur) zastosujemy III zasadę dynamiki.

Zastosujemy II zasadę dynamiki do każdego z poruszających się ciał. W tym celu najpierw sporządzamy diagram sił działających na masę pierwszą i drugą. Dla każdego z ciał wprowadzamy osobny układ współrzędnych \(xy\). Siły działające na ciała i przyspieszenia ciał są reprezentowane przez ich wartości bezwzględne.

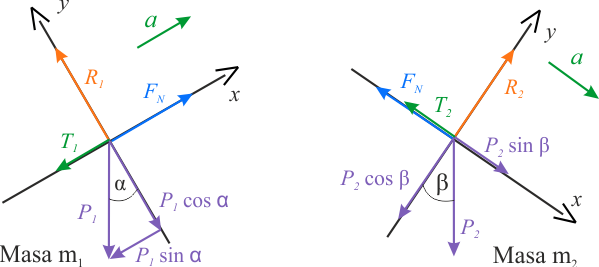
Rysunek


Zakładamy, że siły, których zwrot jest zgodny z kierunkiem ruchu, są dodatnie, natomiast pozostałe mają wartość ujemną. Układ równań dla poruszającego się układu mas wygląda następująco:

Siły działające na masę \(m_1\):

\(\begin{eqnarray} \left\{ \begin{array}{l} \sum F_x= F_N-T_1-P_1\sin\alpha=am_1 \\ \sum F_y= R_1-P_1\cos\alpha=0 \end{array} \right. \end{eqnarray}\)

Siły działające na masę \(m_2\):

\(\begin{eqnarray}  \left\{  \begin{array}{l}  \sum F_x= P_2\sin\beta-F_N-T_2=am_2  \\ \sum F_y= R_2-P_2\cos\beta=0  \end{array}  \right. \end{eqnarray}\)

Po paru otrzymujemy:

\(\displaystyle{a=\frac{m_2g\,(\sin\beta-\mu \cos\beta)-m_1g\,(\sin\alpha+\mu\cos\alpha)}{m_1+m_2}}\)

\(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}} }\)

Siłę tarcia można przedstawić jako \(T=\mu R\), więc, po podstawieniu równania przyjmują postać:

\(\begin{eqnarray} \left\{ \begin{array}{l} F_N-\mu R_1-P_1\sin\alpha=am_1 \\ R_1=P_1\cos\alpha \end{array} \right. \end{eqnarray}\)  \(\begin{eqnarray} \left\{ \begin{array}{l} P_2\sin\beta-F_N-\mu R_2=am_2 \\ R_2=P_2\cos\beta \end{array} \right. \end{eqnarray}\)

Po podstawieniu wartości \(R_1\) i \(R_2\), wyliczonych na podstawie drugich równań obu układów otrzymujemy:

\(\begin{eqnarray} \left\{ \begin{array}{l} F_N-\mu P_1\cos\alpha-P_1\sin\alpha=am_1 \\ P_2\sin\beta-F_N-\mu P_2\cos\beta=am_2 \end{array} \right. \end{eqnarray}\)

Następnie podstawiamy wartości \(P_1=m_1g\) i \(P_2=m_2g\):

\(\begin{eqnarray} \left\{ \begin{array}{l} am_1=F_N-\mu m_1g\cos\alpha-m_1g\sin\alpha \\ am_2=m_2g\sin\beta-F_N-\mu m_2g\cos\beta \end{array} \right. \end{eqnarray}\)

Wyrażenie opisujące przyspieszenie układu wyznaczymy, dodając stronami powyższe równania:

\(\eqalign{a(m_1+m_2) &=-\mu m_1g\cos\alpha-m_1g\sin\alpha+m_2g\sin\beta-\mu m_2g\cos\beta \\ a= &\frac{m_2g\,(\sin\beta-\mu \cos\beta)-m_1g\,(\sin\alpha+\mu\cos\alpha)}{m_1+m_2} \\ a= &\frac{12\cdot 10\,(\sin 45^{\circ}-0,2 \cos 45^{\circ})-5\cdot 10\,(\sin 30^{\circ}+0,2\,\cos 30^{\circ})}{5+12} \\ a= &2\,\mathrm{\frac{m}{s^2}} }\)

Polecenie

Oblicz siłę naciągu nici i wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(F_N=7,4\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(F_N=43,7\,\mathrm{N}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(F_N=11,2\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(F_N=13,8\,\mathrm{N}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Z poprzednio przeprowadzonych rozważań uzyskaliśmy zestaw równań:

  • Siły działające na masę \(m_1\):

\(\begin{eqnarray} \left\{ \begin{array}{l} \sum F_x= F_N-T_1-P_1\sin\alpha=am_1 \\ \sum F_y= R_1-P_1\cos\alpha=0 \end{array} \right. \end{eqnarray}\)

  • Siły działające na masę \(m_2\):

\(\begin{eqnarray}  \left\{  \begin{array}{l}  \sum F_x= P_2\sin\beta-F_N-T_2=am_2  \\ \sum F_y= R_2-P_2\cos\beta=0  \end{array}  \right. \end{eqnarray}\)

Po przekształceniach wykonanych wcześniej otrzymujemy układ równań:

\(\begin{eqnarray} \left\{ \begin{array}{l} am_1=F_N-\mu m_1g\cos\alpha-m_1g\sin\alpha \\ am_2=m_2g\sin\beta-F_N-\mu m_2g\cos\beta \end{array} \right. \end{eqnarray}\)

Po otrzymujemy wyrażenie:

\(\eqalign{F_N= &\frac{m_1m_2g\,(\mu\,(\cos\alpha-\cos\beta)+\sin\alpha+\sin\beta)}{m_1+m_2} \\ F_N= &\frac{5\cdot 12\cdot 10\cdot (0,2\,(\cos 30^{\circ}-\cos 45^{\circ})+\sin 30^{\circ}+\sin 45^{\circ})}{5+12} \\ F_N= &43,7\,\mathrm{N} }\)

Dodając stronami równania obliczyliśmy poprzednio przyspieszenie, które wynosiło:

\(\displaystyle{a=\frac{m_2g\,(\sin\beta-\mu \cos\beta)-m_1g\,(\sin\alpha+\mu\cos\alpha)}{m_1+m_2}}\)

Tą wartość podstawiamy do równania pierwszego \(am_1=F_N-\mu m_1g\cos\alpha-m_1g\sin\alpha\) i otrzymujemy:

\(\displaystyle{\frac{m_2g\,(\sin\beta-\mu \cos\beta)-m_1g\,(\sin\alpha+\mu\cos\alpha)}{m_1+m_2}m_1=F_N-\mu m_1g\cos\alpha-m_1g\sin\alpha }\)

\(\eqalign{F_N &=\frac{m_2g\,(\sin\beta-\mu \cos\beta)-m_1g\,(\sin\alpha+\mu\cos\alpha)}{m_1+m_2}m_1+m_1g(\mu \cos\alpha+\sin\alpha) \\ F_N &=m_1g\frac{m_2\,(\sin\beta-\mu \cos\beta)-m_1\,(\sin\alpha+\mu\cos\alpha)}{m_1+m_2}+\frac{m_1g(\mu \cos\alpha+\sin\alpha)(m_1+m_2)}{m_1+m_2} \\ F_N &=\frac{m_1gm_2(\sin\beta-\mu\cos\beta)-m_1gm_1(\mu\cos\alpha+\sin\alpha)+m_1gm_1(\mu\cos\alpha+\sin\alpha)+m_1gm_2(\mu\cos\alpha+\sin\alpha)}{m_1+m_2} \\ F_N &=\frac{m_1gm_2(\sin\beta-\mu\cos\beta)+m_1gm_2(\mu\cos\alpha+\sin\alpha)}{m_1+m_2} \\ F_N &=\frac{m_1gm_2(\sin\beta-\mu\cos\beta+\sin\alpha+\mu\cos\alpha)}{m_1+m_2} }\)

Odpowiedź

Przyspieszenie ciał wynosi \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}} }\), natomiast siła naciągu nici przyjmuje wartość \(F_N=43,7\,\mathrm{N}\).