Zadanie 3.5.1.1
Podpierana belka
Jednorodna metalowa belka o długości \(L=5\,\mathrm{m}\) i masie \(80\,\mathrm{kg}\) spoczywa na ramionach dwóch mężczyzn. Punkt podparcia belki znajduje się: jeden na jednym końcu, a drugi w odległości \(d=1\,\mathrm{m}\) od drugiego końca. Oblicz siły działające na ramiona mężczyzn.
Wskazówka teoretyczna
Teoria - moment siły
Moment siły względem danej osi
Moment siły względem danej osi obrotu wyrażany jest wzorem:
gdzie \(F_{\perp}\) oznacza składową siły \(F\) leżącą w płaszczyźnie prostopadłej do osi obrotu ciała, zaś \(l\) oznacza ramię działania dla składowej siły \(F_{\perp}\).
Moment siły względem danej osi obrotu wyrażany jest wzorem:
\(M=l\,F_{\perp}\),
gdzie \(F_{\perp}\) oznacza składową siły \(F\) leżącą w płaszczyźnie prostopadłej do osi obrotu ciała, zaś \(l\) oznacza ramię działania dla składowej siły \(F_{\perp}\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- długość belki \(L=5\,\mathrm{m}\),
- masa belki \(m=80\,\mathrm{kg}\),
- odległość od końca belki do drugiego punktu podparcia \(d=1\,\mathrm{m}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- siła działająca na ramiona robotnika pierwszego \(F_1\),
- siła działająca na ramiona robotnika drugiego \(F_2\).
Analiza sytuacji
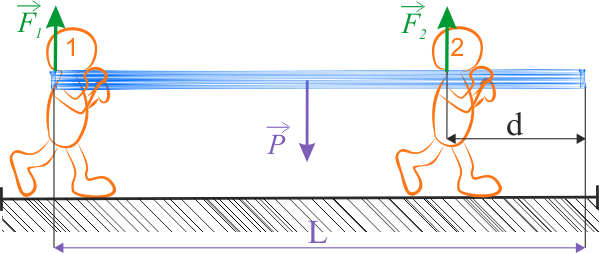
Na rysunku powyżej zostały zaznaczone siły działające na belkę:
- siła ciężkości \(P=mg\) (przyłożona do środka ciężkości belki),
- siły \(F_1\) i \(F_2\), z jakimi ramiona mężczyzn podtrzymują belkę.
Z Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \] wynika, że siła, z jaką belka działa na ramiona mężczyzn, jest równa, co do wartości sile, z jaką ramię działa na belkę. Aby rozwiązać zadanie, wystarczy więc znaleźć wartości sił \(F_1\) i \(F_2\). Belka jest w równowadze, a więc suma sił na nią działających wynosi zero. W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.
\(P-F_1-F_2=0\)
Powyższe równanie zostało zapisane w postaci skalarnej, ponieważ wszystkie trzy siły sa do siebie równoległe. Siły \(F_1\) i \(F_2\) są przeciwnie skierowane do siły \(P\).
W zapisanym równaniu są dwie niewiadome, wynika z tego, że należy zapisać jeszcze jedno równanie. Wykorzystamy fakt, iż punkt przyłożenia siły przez drugiego mężczyznę, jest oddalony od końca belki. W takim przypadku należy rozpatrzeć moment siły. W tym celu narysujmy działające siły na tle osi współrzędnych i zaznaczmy położenia przyłożonych sił.
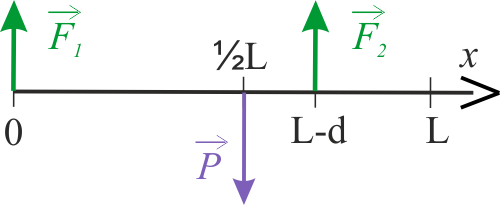
Załóżmy, że przez punkt podparcia belki na ramieniu pierwszego człowieka, przechodzi oś obrotu. Momenty sił względem każdej, a więc i tej szczególnej osi, muszą się zerować i stąd mamy:
\(\displaystyle{P\cdot\frac{L}{2}-F_1\cdot 0-F_2\cdot (L-d)=0 }\)
Moment siły \(F_1\) jest równy zero, gdyż ramię jej działania, przy tak dobranej osi, wynosi zero. Poprzez zapisanie przeciwnych znaków przy składnikach związanych z ciężarem oraz działającymi siłami uwzględniliśmy fakt, iż moment siły \(F_2\) i siły ciężkości „obracają” belkę w przeciwnych kierunkach.
Otrzymaliśmy układ dwóch równań:
\(\begin{eqnarray} \begin{cases} P-F_1-F_2 &=0\\ P\cdot\frac{L}{2}-F_1\cdot 0-F_2\cdot (L-d) &=0 \end{cases} \end{eqnarray} \)
Rozwiązanie
Z równania drugiego, otrzymanego układu równań, wyznaczamy wartość siły \(F_2\).
\(\displaystyle{P\cdot\frac{L}{2}=F_2(L-d) }\)
\(\displaystyle{F_2=mg\,\frac{L}{2\,(L-d)} }\)
Na podstawie równania pierwszego wyznaczamy wartość siły \(F_1\).
\(F_1=P-F_2\)
\[\displaystyle{F_1=P-P\,\frac{L}{2\,(L-d)} }\] \[\displaystyle{F_1=P\left (1-\frac{L}{2\,(L-d)}\right ) }\] \[F_1=P\left ( \frac{2(L-d)}{2(L-d)}-\frac{L}{2(L-d)} \right )\]
\(\displaystyle{F_1=mg\cdot \frac{L-2d}{2\,(L-d)} }\)
Podstawiając wartości liczbowe otrzymujemy:
\(\displaystyle{F_2=80\cdot 10\cdot\frac{5}{2\cdot (5-1)}=500\,\mathrm{N} }\) \(\displaystyle{F_1=80\cdot 10\cdot \frac{5-2}{2\cdot(5-1)}=300\,\mathrm{N} }\)
Odpowiedź
Na pierwszego mężczyznę działa siła \(F_1=300\,\mathrm{N}\), na drugiego \(F_2=500\,\mathrm{N}\).