Zadanie 3.5.1.2
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.5. Statyka
  4. 3.5.1 Nauka
  5. Zadanie 3.5.1.2

 Zadanie 3.5.1.2

Wiszący przedmiot
Ciężarek o masie \(m=4\,\mathrm{kg}\) zawieszono na dwóch drutach tworzących z poziomem kąty \(\alpha=30^{\circ}\) oraz \(\beta=45^{\circ}\). Wyznacz siły naprężające druty.

Rysunek

 Wskazówka teoretyczna

 Teoria - zasady dynamiki
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]
Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
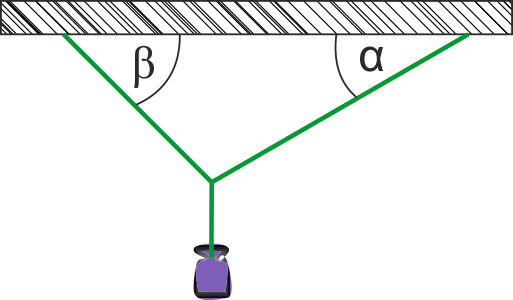
- masa ciężarka \(m=4\,\mathrm{kg}\),
- kąt, pod jakim zawieszony jest drut po prawej stronie ciężarka \(\alpha=30^{\circ}\),
- kąt, pod jakim zawieszony jest drut po lewej stronie ciężarka \(\beta=45^{\circ}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- siła naprężająca drut po stronie prawej ciężarka \(F_{N1}\),
- siła naprężająca drut po stronie lewej ciężarka \(F_{N2}\).

Analiza sytuacji

Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero. Graficzne przedstawienie tej zasady pokazane jest na rysunku poniżej. Złożenie wszystkich sił tworzy kontur zamknięty, czyli siły te wzajemnie się redukują.

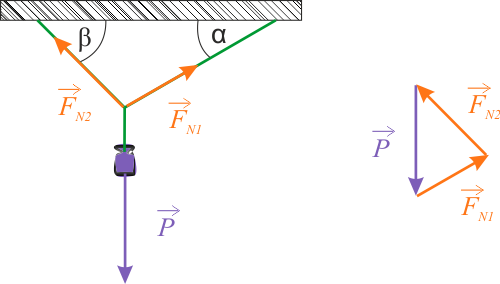
Rysunek

W celu wykonania obliczeń, należy rozłożyć siły działające w układzie na ich składowe leżące wzdłuż osi \(OX\) i \(OY\).

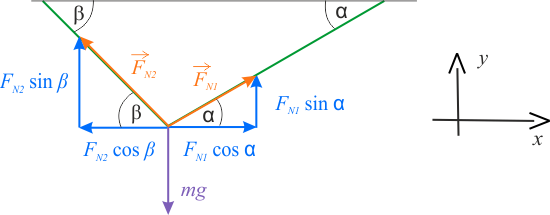
Rysunek

\[ \sum{F}=0 \Rightarrow \left\{\begin{matrix} \sum{F_X}=0 \\ \sum{F_Y}=0 \end{matrix}\right. \Rightarrow \left\{\begin{matrix} F_{N1x}-F_{N2x}=0 \\ F_{N1y}+F_{N2y}-mg=0 \end{matrix}\right. \]
 W pierwszym równaniu występują siły działające wzdłuż osi \(OX\), są to dwie składowe iksowe sił \(F_{N1}\) i \(F_{N2}\). Drugie równanie przedstawia siły działające wzdłuż osi \(OY\) - dwie składowe igrekowe sił \(F_{N1}\) i \(F_{N2}\) oraz siła ciężkości. Składowe dwóch sił można obliczyć za pomocą funkcji trygonometrycznych.  

\( \left\{ \begin{matrix} F_{N1}\cos\alpha-F_{N2}\cos\beta &=0 \\ F_{N1}\sin\alpha+F_{N2}\sin\beta-mg &=0 \end{matrix}\right. \)

Rozwiązanie

Z równania pierwszego wyznaczmy siłę \(F_{N1}\).

\(F_{N1}\cos\alpha=F_{N2}\cos\beta\)

\(\displaystyle{F_{N1}=\frac{F_{N2}\cos\beta}{\cos\alpha} }\)

Z równania drugiego otrzymamy wyrażenie opisujące siłą \(F_{N2}\).

\(F_{N2}\sin\beta=mg-F_{N1}\sin\alpha \)

\(\displaystyle{F_{N2}=\frac{mg}{\sin\beta}-F_{N1}\frac{\sin\alpha}{\sin\beta} }\)

Za \(F_{N1}\) podstawiamy poprzednio wyprowadzoną wartość i otrzymujemy:

\(\displaystyle{F_{N2}=\frac{mg}{\sin\beta}-F_{N2}\frac{\cos\beta}{\cos\alpha}\frac{\sin\alpha}{\sin\beta} }\)

Po  \[\displaystyle{F_{N2}+F_{N2}\frac{\cos\beta}{\sin\beta}\cdot\operatorname{tg}{\alpha}=\frac{mg}{\sin\beta} }\] \[\displaystyle{F_{N2}\left ( 1+\frac{\cos\beta}{\sin\beta}\cdot \operatorname{tg}{\alpha} \right )=\frac{mg}{\sin\beta} }\] \[\displaystyle{F_{N2}\cdot \frac{\sin\beta + \cos\beta\cdot \operatorname{tg}{\alpha}}{\sin\beta} =\frac{mg}{\sin\beta} }\] \[\displaystyle{F_{N2} =\frac{mg}{\sin\beta}\cdot \frac{\sin\beta }{\sin\beta + \cos\beta\cdot \operatorname{tg}{\alpha}} }\]  otrzymujemy:

\(\displaystyle{F_{N2}=\frac{mg}{\sin\beta+\cos\beta\cdot \operatorname{tg}{\alpha}} }\) 

\(\displaystyle{F_{N1}=\frac{mg}{\sin\beta+\cos\beta\cdot \operatorname{tg}{\alpha}}\cdot \frac{\cos\beta}{\cos\alpha} }\)

Po podstawieniu wartości liczbowych mamy:

\(\displaystyle{F_{N2}=\frac{4\cdot 10}{\sin 45^{\circ}+\cos 45^{\circ} \cdot \operatorname{tg}{30^{\circ}}}=35,86\,\mathrm{N} }\)

\(\displaystyle{F_{N1}=\frac{4\cdot 10}{\sin 45^{\circ}+\cos 45^{\circ}\cdot \operatorname{tg}{30^{\circ}}}\cdot \frac{\cos 45^{\circ}}{\cos 30^{\circ}}=29,28 \,\mathrm{N} }\)

Odpowiedź

Siły naprężające drut wynoszą odpowiednio: dla drutu po prawej stronie \(\displaystyle{F_{N1}=29,28 \,\mathrm{N} }\) oraz dla drutu po lewej stronie \(\displaystyle{F_{N2}=35,86\,\mathrm{N} }\).