Zadanie 3.5.1.3
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.5. Statyka
  4. 3.5.1 Nauka
  5. Zadanie 3.5.1.3

 Zadanie 3.5.1.3

Dwie piłki w cylindrze
W pojemniku o cylindrycznym kształcie umieszczono dwie piłki o promieniach \(R=0,35\,\mathrm{m}\) i \(r=0,25\,\mathrm{m}\) oraz masach \(m_1=0,55\,\mathrm{kg}\) i \(m_2=0,3\,\mathrm{kg}\). Wyznacz siły działające na piłki w punktach styku (pomiędzy piłkami oraz piłek ze ściankami pojemnika). Średnica pojemnika wynosi \(d=1\,\mathrm{m}\).

 Wskazówka teoretyczna

 Teoria - zasady dynamiki
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- promień pierwszej piłki \(R=0,35\,\mathrm{m}\),
- masa pierwszej piłki \(m_1=0,55\,\mathrm{kg}\),
- promień drugiej piłki \(r=0,25\,\mathrm{m}\),
- masa drugiej piłki \(m_2=0,3\,\mathrm{kg}\),
- średnica pojemnika \(d=1\,\mathrm{m}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\)

Szukane:
- siła nacisku pierwszej piłki na ściankę pojemnika \(F_1\),
- siła nacisku drugiej piłki na ściankę pojemnika \(F_2\),
- siła nacisku drugiej piłki na dno pojemnika \(F_3\),
- siła nacisku pomiędzy piłkami \(F_4\).

Analiza sytuacji

Dwie piłki umieszczone w cylindrycznym pojemniku, wywierają nacisk na ścianki w punktach styku oraz wzajemnie na siebie. Piłka o większym promieniu naciska na lewa ściankę pojemnika siłą \(\vec{F_1}\) oraz na piłkę, leżącą niżej, siłą \(\vec{F_4}\). Piłka o promieniu \(r\) naciska na dno oraz prawą ściankę naczynia siłami \(\vec{F_3}\) i \(\vec{F_2}\). Na tę piłkę wywiera również nacisk druga piłka - siła \(\vec{F_4}\).

Poniżej znajduje się rysunek, obrazujący działające siły.

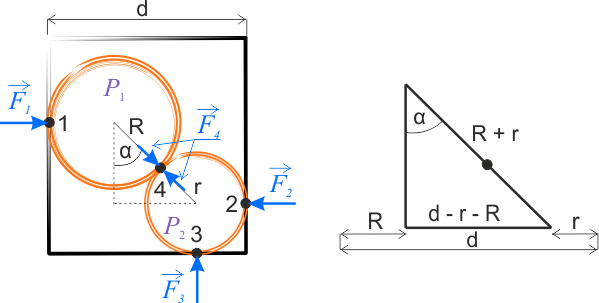
Rysunek


Na rysunku zaznaczone są siły reakcji ścianek pojemnika na nacisk piłek. Są to siły o takiej samej wartości, co siły nacisku piłek na ścianki.

Rozpiszmy równania kolejno dla piłek.

Piłka po lewej stronie:

\(\begin{eqnarray} \begin{cases} F_1-F_{4x} &=0\\ -P_1+F_{4y} &=0 \end{cases} \end{eqnarray} \)

\(\begin{eqnarray} \begin{cases} F_1-F_{4}\sin\alpha &=0\\ -P_1+F_{4}\cos\alpha &=0 \end{cases} \end{eqnarray} \)

Piłka po prawej stronie:

\(\begin{eqnarray} \begin{cases} F_{4x}-F_2 &=0\\ -P_2-F_{4y}+F_3 &=0 \end{cases} \end{eqnarray} \)

\(\begin{eqnarray} \begin{cases} F_{4}\sin\alpha-F_2 &=0\\ -P_2-F_{4}\cos\alpha+F_3 &=0 \end{cases} \end{eqnarray} \)

Rozwiązanie

Porównując równania zapisane dla dwóch piłek

\(\begin{eqnarray} \begin{cases} F_1=F_{4}\sin\alpha \\ P_1=F_{4}\cos\alpha \end{cases} \end{eqnarray} \)     \(\begin{eqnarray} \begin{cases} F_2=F_{4}\sin\alpha \\ F_3=P_2+F_{4}\cos\alpha \end{cases} \end{eqnarray} \)
mamy:
\(F_1=F_2=F_{4}\sin\alpha\)

\(\displaystyle{F_4=\frac{P_1}{\cos\alpha}=\frac{m_1g}{\cos\alpha} }\)

Kąt \(\alpha\) obliczamy z prostokątnego trójkąta pokazanego na powyższym rysunku.

\(\displaystyle{\sin\alpha=\frac{d-r-R}{R+r} }\)

Podstawiając wartości liczbowe mamy

\(\displaystyle{\sin\alpha=\frac{1-0,25-0,35}{0,35+0,25}=\frac{2}{3} }\)

\(\arcsin 0,666667=41,8 ^{\circ}\)

\(\displaystyle{F_4=\frac{0,55\cdot 10}{\cos 41,8^{\circ}}=7,4\,\mathrm{N} }\)

\(F_1=F_2=7,4\cdot \sin 41,8^{\circ}=4,9 \,\mathrm{N} \)

\(F_3=0,3\cdot 10+7,4\cdot \cos 41,8^{\circ}=8,5 \,\mathrm{N}\)

Odpowiedź

Siły nacisku wynoszą:
- siła nacisku pierwszej piłki na ściankę pojemnika \(F_1=4,9 \,\mathrm{N}\),
- siła nacisku drugiej piłki na ściankę pojemnika \(F_2=4,9 \,\mathrm{N}\),
- siła nacisku drugiej piłki na dno pojemnika \(F_3=8,5\,\mathrm{N}\),
- siła nacisku pomiędzy piłkami \(F_4=7,4\,\mathrm{N}\).