Zadanie 3.5.1.4
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.5. Statyka
  4. 3.5.1 Nauka
  5. Zadanie 3.5.1.4

 Zadanie 3.5.1.4

Siły działające ne element konstrukcyjny
Siły o wartościach \(F_1=250\,\mathrm{N}\), \(F_2=100\,\mathrm{N}\) i \(F_3=20\,\mathrm{N}\) działają na lekki element konstrukcji przedstawiony na rysunku. Element ten będzie w równowadze, jeśli przyłożymy siłę w punkcie \(A\). Mając dane odległości (wartości podane są na rysunku) wyznacz wartość i kierunek siły \(F\) oraz położenie punktu \(A\) - odległość \(x\). Co się zmieni, jeśli odległość \(d\) zwiększymy \(12\) razy?

 Wskazówka teoretyczna

 Teoria - moment siły
Moment siły względem danej osi

Moment siły względem danej osi obrotu wyrażany jest wzorem:

\(M=l\,F_{\perp}\),

gdzie \(F_{\perp}\) oznacza składową siły \(F\) leżącą w płaszczyźnie prostopadłej do osi obrotu ciała, zaś \(l\) oznacza ramię działania dla składowej siły \(F_{\perp}\).
Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- wartość pierwszej siły \(F_1=250\,\mathrm{N}\),
- wartość drugiej siły \(F_2=100\,\mathrm{N}\),
- wartość trzeciej siły \(F_3=20\,\mathrm{N}\),
- odległości między punktami przyłożeń sił: \(a=1\,\mathrm{m}\), \(b=3\,\mathrm{m}\), \(c=2\,\mathrm{m}\) oraz \(d=0,5\,\mathrm{m}\).

Szukane:
- wartość siły \(F\),
- kąt określający kierunek siły \(\alpha\),
- odległość \(x\) - położenie punktu \(A\).

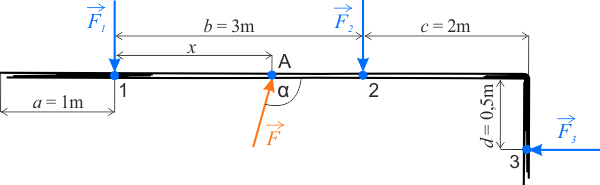
Analiza sytuacji

Na element konstrukcyjny działają siły w różnych kierunkach - poziomym \(F_3\), pionowym \(F_1\) oraz \(F_2\) i skośnym \(F\). Według treści zadania element pozostaje w równowadze, więc zgodnie z  W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.  suma działających sił wyniesie zero. Rozpiszmy więc, jakie siły działają na element w pionie oraz w poziomie.

Siły działające pionowo: \(-F_1-F_2+F_y=0\) oraz poziomo: \(F_x-F_3=0\).

Siłę \(F\) można rozłożyć na składowe, w tym celu wprowadźmy kąt \(\beta=180^{\circ}-\alpha\).

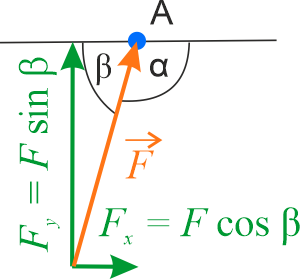
Rysunek

 wynoszą, więc \[\eqalign{F_x &=F\cos\beta \\ F_y &=F\sin\beta}\] 

Układ równań opisujący działające siły, zgodnie z I zasada dynamiki, ma postać:

\(\begin{eqnarray} \begin{cases} F\sin\beta &=F_1+F_2\\ F\cos\beta &=F_3 \end{cases} \end{eqnarray} \)

Zastanówmy się teraz nad momentami sił, działających na element konstrukcji. Załóżmy, że oś obrotu przechodzi przez punkt \(1\). Niech siły powodujące obrót elementu zgodnie z ruchem wskazówek będą dodatnie, a siły powodujące obrót w lewo - ujemne.

\(F_1\cdot 0-F_y\cdot x+F_2\cdot b+F_3\cdot d=0\)

\(F\sin\beta x=F_2\cdot b+F_3\cdot d\)

\(\displaystyle{x=\frac{F_2\cdot b+F_3\cdot d}{F\sin\beta} }\)

Rozwiązanie

W celu wyznaczenie kąta określającego kierunek przyłożenia siły \(F\), należy podzielić stronami równania

\(\begin{eqnarray} \begin{cases} F\sin\beta &=F_1+F_2\\ F\cos\beta &=F_3  \end{cases} \end{eqnarray} \)

\(\displaystyle{ \frac{F\sin\beta}{F\cos\beta}=\frac{F_1+F_2}{F_3} }\)

\(\displaystyle{\operatorname{tg}{\beta}=\frac{F_1+F_2}{F_3} }\)

\(\displaystyle{\operatorname{tg}{\beta}=\frac{250+100}{20}=17,5 }\)

Funkcja tangens przyjmuje wartość \(17,5\) dla kąta \(\beta=86,7^{\circ}\). Wartość kąta przyłożenia siły \(F\) wynosi \(\alpha=180^{\circ}-86,7^{\circ}=93,3^{\circ} \)

Wartość siły możemy wyznaczyć na podstawie równania pierwszego

\(\displaystyle{F=\frac{F_1+F_2}{\sin\beta} }\)

\(\displaystyle{F=\frac{250+100}{\sin 93,3^{\circ}}=350,6 \,\mathrm{N} }\)

Wyznaczenie odległości \(x\) wymaga użycia równania wyprowadzonego na podstawie analizy momentów sił:

\(\displaystyle{x=\frac{F_2\cdot b+F_3\cdot d}{F\sin\beta} }\)

\(\displaystyle{x=\frac{100\cdot 3+20\cdot 0,5}{350,6 \cdot \sin 93,3^{\circ}}=0,9\,\mathrm{m} }\)

Odległość \(d\) pojawiła się tylko w równaniu, pozwalającym obliczyć odległość \(x\). Zmiana wartości \(d\) na \(d_2=0,5\cdot 12=6\,\mathrm{m}\) spowoduje wzrost odległości \(x\).

\(\displaystyle{x_2=\frac{100\cdot 3+20\cdot 6}{350,6 \cdot \sin 93,3^{\circ}}=1,2\,\mathrm{m} }\)

Odpowiedź

Wartość siły \(F\) wynosi \(350\,\mathrm{N}\), kąt \(\alpha\) ma miarę \(93,3^{\circ}\), natomiast punkt przyłożenia siły leży w odległości \(x=0,9\,\mathrm{m}\). Wydłużenie odległości \(d\) dwunastokrotnie spowoduje tylko zmianę położenia punkt przyłożenia siły \(x_2=1,2\,\mathrm{m}\).