Zadanie 3.5.1.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.5. Statyka
  4. 3.5.1 Nauka
  5. Zadanie 3.5.1.5

 Zadanie 3.5.1.5

Podpory
Wyznacz siły reakcji w podporach \(A\) i \(B\) belki pokazanej na rysunku poniżej. Wartości działających sił wynoszą \(F_1=3\,\mathrm{kN}\) oraz \(F_2=600\,\mathrm{N}\). Kąty, pod jakimi skierowane są siły, wynoszą \(\alpha_1=30^{\circ}\) i \(\alpha_2=45^{\circ}\).

 Wskazówka teoretyczna

 Teoria - moment siły
Moment siły względem danej osi

Moment siły względem danej osi obrotu wyrażany jest wzorem:

\(M=l\,F_{\perp}\),

gdzie \(F_{\perp}\) oznacza składową siły \(F\) leżącą w płaszczyźnie prostopadłej do osi obrotu ciała, zaś \(l\) oznacza ramię działania dla składowej siły \(F_{\perp}\).
Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

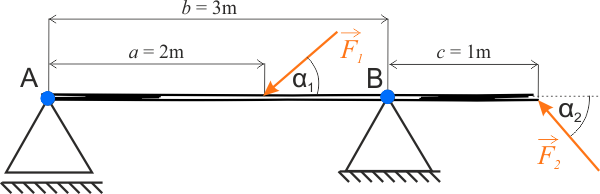
Dane:
- wartość pierwszej siły \(F_1=3\,\mathrm{kN}\),
- wartość drugiej siły \(F_2=600\,\mathrm{N}\),
- odległości między punktami przyłożeń sił: \(a=2\,\mathrm{m}\), \(b=3\,\mathrm{m}\) oraz \(c=1\,\mathrm{m}\),
- kąt, pod jakim działa siła \(F_1\): \(\alpha_1=30^{\circ}\),
- kąt, pod jakim działa siła \(F_2\): \(\alpha_2=45^{\circ}\).

Szukane:
- wartość siły reakcji \(R_{bx}\),
- wartość siły reakcji \(R_{by}\),
- wartość siły reakcji \(R_{a}\).

Analiza sytuacji

Belka podparta jest na dwóch podporach. Podpora po lewej stronie jest przesuwna, więc w punkcie \(A\) działa siła reakcji \(R_a\) skierowana pionowo do góry. Druga podpora jest nieprzesuwna, co za tym idzie, w punkcie \(B\) działają siły reakcji \(R_{bx}\) oraz \(R_{by}\).  Na poniższym rysunku przedstawiono również składowe sił \(F_1\) oraz \(F_2\).

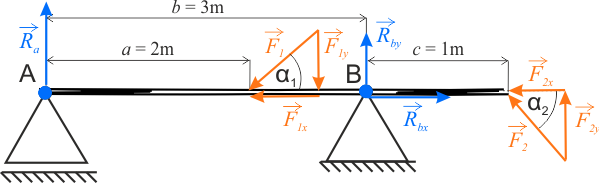
Rysunek


Mając rozrysowane siły, możemy zapisać, zgodnie z  W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.  , siły działające na nieruchomą belkę.

\(\begin{eqnarray} \begin{cases} \sum F_x=-F_{1x}+R_{bx}-F_{2x} &=0\\ \sum F_y=R_a-F_{1y}+R_{by}+F_{2y} &=0 \end{cases} \end{eqnarray} \)

Rozpisując składowe sił otrzymujemy:

\(\begin{eqnarray} \begin{cases} R_{bx} &=F_1\cdot \cos \alpha_1+F_2\cdot \cos \alpha_2 \\ R_a &= F_1\sin \alpha_1-F_2\sin \alpha_2-R_{by} \end{cases} \end{eqnarray} \)

Rozpatrzmy teraz momenty sił. Załóżmy, że oś obrotu przechodzi przez punkt \(A\).

\(-F_{1y}\cdot a+R_{by}\cdot b+F_{2y}\cdot (b+c)=0\)

Rozpisując składowe sił otrzymujemy:

\(-F_1\sin \alpha_1\cdot a+R_{by}\cdot b+F_2\sin \alpha_2\cdot (b+c)=0\)

Rozwiązanie

Siłę \(R_{bx}\) wyznaczamy z pierwszego równania układu równań.

\(R_{bx} =F_1\cdot \cos \alpha_1+F_2\cdot \cos \alpha_2\)

\(R_{bx} =3000\cdot \cos 30^{\circ}+600\cdot \cos 45^{\circ}=3022\,\mathrm{N}\)

Wartość siły \(R_{by}\) najwygodniej jest wyznaczyć z równania opisującego momenty sił:

\(R_{by}\cdot b=F_1\sin \alpha_1\cdot a-F_2\sin \alpha_2\cdot (b+c)\)

\(\displaystyle{R_{by}=F_1\frac{a}{b}\sin \alpha_1-F_2\frac{b+c}{b}\sin \alpha_2 }\)

\(\displaystyle{R_{by}=3000\cdot\frac{2}{3}\cdot\sin 30^{\circ}-600\cdot \frac{3+1}{3}\cdot\sin 45^{\circ}=434\,\mathrm{N} }\)

Wartość siły \(R_{a}\) obliczamy z równania drugiego układu równań

\(R_a = F_1\sin \alpha_1-F_2\sin \alpha_2-R_{by}\)
 \[\displaystyle{R_a = F_1\sin \alpha_1-F_2\sin \alpha_2-F_1\frac{a}{b}\sin \alpha_1+F_2\frac{b+c}{b}\sin \alpha_2 }\] \[\displaystyle{R_a = F_1\sin \alpha_1\cdot(1-\frac{a}{b})+F_2\sin \alpha_2\cdot \left (\frac{b+c}{b}-1\right ) }\] 
\(\displaystyle{R_a = F_1\sin \alpha_1\cdot \left (\frac{b-a}{b}\right )+F_2\sin \alpha_2\cdot \left (\frac{c}{b}\right ) }\)

\(\displaystyle{R_a = 3000\cdot\sin 30^{\circ}\cdot\left (\frac{3-2}{3}\right )+600\cdot \sin 45^{\circ}\cdot \left (\frac{1}{3}\right )=641\,\mathrm{N} }\)

Odpowiedź

Siły reakcji w podporach wynoszą \(R_{bx}=3,022\,\mathrm{kN}\), \(R_{by}=434\,\mathrm{N}\) oraz \(R_{a}=641\,\mathrm{N}\).