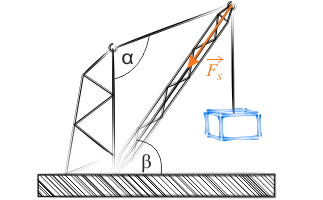
Zadanie 3.5.2.1
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 3. Zasady dynamiki
  3. 3.5. Statyka
  4. 3.5.2 Trening
  5. Zadanie 3.5.2.1
DOI: 10.37190/OZE-FizykaCw1-r3

 Zadanie 3.5.2.1

Dźwig
Wyznacz maksymalną masę, którą można zawiesić na linie dźwigu oraz siłę ściskającą \(F_S\) w umocowanym przegubowo wysięgniku, jeśli dopuszczalne napięcie w linie wynosi \(F_m=150\,\mathrm{kN}\), a kąt \(\alpha=115^{\circ}\).

 Rysunek

Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- dopuszczalne napięcie liny \(F_m=150\,\mathrm{kN}\),
- kąt nachylenia liny do konstrukcji dźwigu \(\alpha=110^{\circ}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- maksymalna masa, którą można zawiesić na linie \(m_m\),
- siła ściskająca wysięgnik \(F_S\).

Odpowiedź

Maksymalna masa, którą można zawiesić na linie dźwigu wynosi \(15\) ton, a siła ściskającą wynosi \(253\,\mathrm{kN}\).

Polecenie

Oblicz maksymalną masę, którą można zawiesić na linie. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(m_m=150\,\mathrm{ton}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(m_m=15\,\mathrm{ton}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(m_m=1,5\,\mathrm{tony}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(m_m=150\,\mathrm{kg}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Maksymalną masę obliczamy z zależności opisującej ciężar \(P=mg\). Siła ciężkości, na podstawie  Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie.   , jest równa sile naciągającej linę.

\(F_m=m_mg\)

\(\displaystyle{m_m=\frac{F_m}{g} }\)

\(\displaystyle{m_m=\frac{150000}{10}=15000\,\mathrm{kg} }\)

Polecenie

Oblicz siłę ściskającą wysięgnik. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(165\,\mathrm{kN}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(215\,\mathrm{kN}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(253\,\mathrm{kN}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(303\,\mathrm{kN}\)

Odpowiedź nieprawidłowa

Rozwiązanie

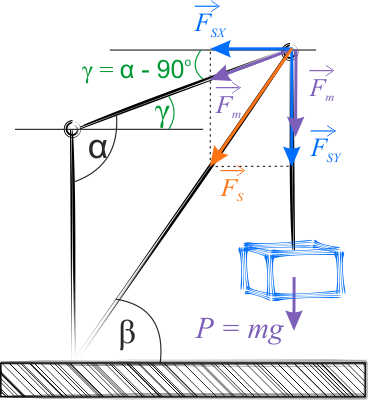
Na rysunku przedstawiono maksymalną siłę \(F_m\), jaka może naciągnąć linę i nie doprowadzić do jej zniszczenia. Wzdłuż wysięgnika działa siła ściskająca \(F_S\), którą mamy obliczyć. Siłę tę rozłożono na dwie składowe \(F_{SX}\) oraz \(F_{SY}\). Na rysunku zaznaczono jeszcze kąt \(\gamma=\alpha-90^{\circ}\), który zostanie użyty do obliczeń.

Składową \(F_{SX}\) można obliczyć następująco:

\(F_{SX}=-F_m\cdot \cos(\alpha-90^{\circ}) \)

\(F_{SX}=-150\,000\cdot \cos(115^{\circ}-90^{\circ})=-135\,946\,\mathrm{N} \)
 Wzdłuż osi \(OX\) działa tylko składowa iksowa siły naciągającej linę i stąd mamy \(F_{mX}=F_{SX}\). 
W osi pionowej działają dwie siły: \(F_m\) - pokazana na pionowej części liny oraz \(F_{mY}\) - igrekowa składowa siły \(F_m\) zaznaczonej wzdłuż nachylonej części liny.

\(F_{SY}=-F_m-F_m\cdot \sin(\alpha-90^{\circ})\)

\(F_{SY}=-150\,000\cdot (1+\sin(115^{\circ}-90^{\circ}))=-213\,393\,\mathrm{N} \)

Wektor wypadkowy wyznaczymy z \(F_S=\sqrt{F_{SX}^2+F_{SY}^2}=253\,017\,\mathrm{N} \)

Rysunek

Odpowiedź

Maksymalna masa, którą można zawiesić na linie dźwigu wynosi \(15\) ton, a siła ściskającą wynosi \(253\,\mathrm{kN}\).