Zadanie 3.5.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
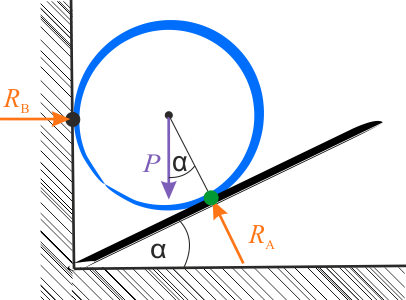
- masa beczki \(m=300\,\mathrm{kg}\),
- kąt nachylenia beczki \(\alpha=30^{\circ}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- siła, z jaką beczka naciska na deskę \(R_A\),
- siła, z jaką beczka naciska na ścianę \(R_B\).
Odpowiedź
Beczka naciska na deskę z siłą \(3464\,\mathrm{N}\), zaś nacisk na ścianę wynosi \(1732\,\mathrm{N}\).
Polecenie
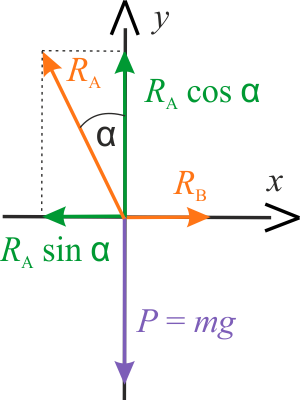
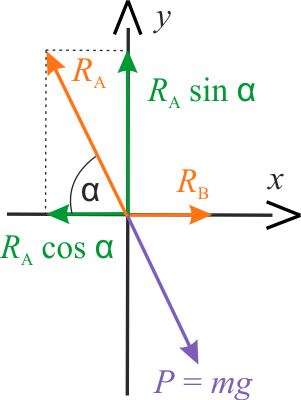
Zastanów się, jak rozrysować siły działające na beczkę i punkty styku, w układzie współrzędnych. Narysuj szkic, a następnie wybierz jedną prawidłową ilustrację, wśród dwóch przedstawionych poniżej.
Polecenie
Oblicz siłę, z jaką beczka naciska na deskę \(R_A\). Wybierz jedną prawidłową odpowiedź, wśród czterech przedstawionych poniżej.
\(R_A=3464\,\mathrm{N}\)
\(R_A=2939\,\mathrm{N}\)
Rozwiązanie
Suma sił działających wzdłuż osi \(x\) wyniesie zero (beczka pozostaje w spoczynku): \(R_B-R_A\sin\alpha=0\).
Wzdłuż osi \(y\) działają następujące siły: \(R_A\cos\alpha-P=0\).
Drugie równanie pozwala, w łatwy sposób, wyznaczyć siłę \(R_A\)
Polecenie
Oblicz siłę, z jaką beczka naciska na ścianę \(R_B\). Wybierz jedną prawidłową odpowiedź, wśród czterech przedstawionych poniżej.
Rozwiązanie
Równania opisujące działające siły maja następująca postać:
\[\displaystyle{R_A=\frac{mg}{\cos\alpha} }\] \[R_B=R_A\sin\alpha\] \[\displaystyle{R_B=\frac{mg}{\cos\alpha}\sin\alpha }\]
Odpowiedź
Beczka naciska na deskę z siłą \(3464\,\mathrm{N}\), zaś nacisk na ścianę wynosi \(1732\,\mathrm{N}\).