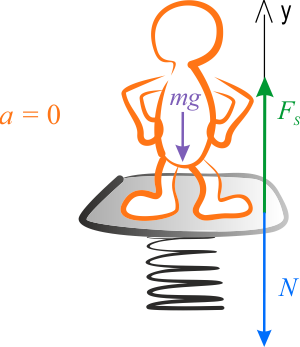Zadanie 3.6.1.1
W windzie osobowej, na wadze sprężynowej, stoi człowiek o masie \(80\,\mathrm{kg}\). Jakie jest wskazanie wagi, gdy winda porusza się:
a) ze stałą prędkością w górę,
b) z przyspieszeniem \(\displaystyle{a=\frac{g}{4}}\) w górę.
Wskazówka teoretyczna
Inercjalny układ odniesienia można również zdefiniować jako taki układ, w którym nie pojawiają się pozorne siły bezwładności.
Układ nieinercjalny – układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.
Transformacja równań ruchu z układu inercjalnego do układu nieinercjalnego powoduje, że w równaniu ruchu, zapisanym w układzie nieinercjalnym, pojawiają się dodatkowe wyrazy, których wartość zależy od ruchu układu nieinercjalnego względem inercjalnego. Wyrazy te mają wymiar siły i dlatego mówimy, że w takim układzie występują pozorne siły. Nazywane są one siłami bezwładności i należą do nich, np. siła odśrodkowa i siła Coriolisa.
Teoria - rozwinięcie
Układy, w których obowiązuje pierwsza i druga zasada dynamiki są układami inercjalnymi. Za układy inercjalne uważa się układy nieruchome względem odległych gwiazd lub poruszające się ze stałymi prędkościami względem tych gwiazd. Każdy układ odniesienia poruszający się ze stałą prędkością względem jakiegoś układu inercjalnego, będzie również układem inercjalnym.
Każdy układ, który porusza się ze zmienną prędkością (co do wartości lub kierunku prędkości) względem pewnego układu inercjalnego nazywamy układem nieinercjalnym.
Może to być układ, który:
- porusza się po linii prostej, ale ze zmienną wartością prędkości; np. układ związany z przyspieszającym lub hamującym samochodem (jeżeli układ związany z Ziemią będziemy traktować, jako układ inercjalny),
- porusza się ze stałą, co do wartości, prędkością po torze krzywoliniowym, np. samochód jadący ze stałą prędkością na zakręcie,
- obraca się, np. karuzela.
Komentarz: W zadaniach korzystamy zazwyczaj z układu związanego z Ziemią. Układ ten traktujemy, jako układ inercjalny. Można zapytać, czy słusznie skoro Ziemia się obraca? Rzeczywiście, ściśle rzecz biorąc układ związany z Ziemią (powierzchnią Ziemi) nie jest układem inercjalnym, gdyż Ziemia względem odległych gwiazd obraca się wokół własnej osi. Efekty z tym związane są bardzo małe i w wielu przypadkach możemy je pominąć.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa człowieka \(m=80\,\mathrm{kg}\),
- przyspieszenie windy \(\displaystyle{a=\frac{g}{4}=2,5\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- wskazanie wagi, czyli siła nacisku człowieka na wagę \(N\).
Analiza sytuacji - punkt a)
Jeżeli winda porusza się ze stałą prędkością w górę, to z taką samą prędkością porusza się człowiek w windzie. Wypadkowa siła \(F_w\), działająca na człowieka, musi być więc równa zeru. Ponieważ wiemy, że na człowieka działa siła ciężkości \(P=mg\) w dół, więc sprężyna wagi musi działać siłą sprężystości \(F_s\) w górę, mającą dokładnie taką samą wartość. Waga z kolei wskazuje siłę nacisku \(N\), którą człowiek działa na wagę. Z III zasady dynamiki jest ona równa, co do wartości, sile \(F_s\), a tym samym ciężarowi \(P\).
Iformacja
Poniżej znajduje się animacja, która ilustruje, jak zmieniają się wskazania wagi, na której jest człowiek, stojącej w windzie podczas postoju, ruszania oraz hamowania. Pod obrazkiem znajduje się okrągły przycisk, który uruchamia animację.
Analiza sytuacji - punkt b)
Układ inercjalny
W układzie inercjalnym na człowieka działa siła ciężkości \(P\) – w dół oraz siła sprężystości sprężyny \(F_s\) – w górę. Zgodnie z III zasadą dynamiki człowiek działa na wagę siłą nacisku \(N\) o tej samej wartości co wartość siły \(F_s\).
Zadanie rozwiążemy podobnie, jak w punkcie a) z tym, że teraz siła wypadkowa, działająca na człowieka jest taka, aby z II drugiej zasady dynamiki, nadać mu przyspieszenie takie, jakie ma winda, czyli \(a\) w górę. Jeżeli jako dodatni wybierzemy kierunek w górę, to mamy:
\(N= m\,(g+a)\)
Analiza sytuacji - punkt b)
Układ nieinercjalny
Potraktujmy windę jako układ nieinercjalny, poruszający się z przyspieszeniem \(a\) w górę. Człowiek znajdujący się w windzie jest w tym układzie w spoczynku, jednakże w bilansie wszystkich sił działających na człowieka, należy uwzględnić siłę bezwładności o wartości
Odpowiedź
W przypadku, gdy winda porusza się ze stałą prędkością w górę, człowiek działa na wagę siłą \(N=800\,\mathrm{N}\), więc waga wskaże \(80\,\mathrm{kg}\).
W drugim przypadku, gdy winda porusza się ze stałym przyspieszeniem w górę, człowiek działa na wagę siłą \(N=1000\,\mathrm{N}\), więc waga wskaże \(100\,\mathrm{kg}\).