Zadanie 3.6.1.2
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.6. Nieinercjalne układy odniesienia
  4. 3.6.1 Nauka
  5. Zadanie 3.6.1.2

 Zadanie 3.6.1.2

Poruszający się klin
Klin o masie \(M=3\,\mathrm{kg}\), wysokości \(h=1\,\mathrm{m}\) i długości podstawy \(L=2\,\mathrm{m}\) spoczywał na doskonale gładkim stole. Na jego nachylonej powierzchni położono klocek o masie \(m = 2\,\mathrm{kg}\), a następnie klin wprawiono w przyspieszenie w kierunku, jak na rysunku. Jaka może być wartość przyspieszenia klina, aby klocek był względem niego nieruchomy? Przyjmij, że współczynnik tarcia między klinem a klockiem wynosi \(0,2\). Zadanie rozwiąż w układzie nieinercjalnym związanym z poruszającym się klinem.
Rysunek

 Wskazówka teoretyczna

 Teoria - układ inercjalny i nieinercjalny
Układ inercjalny (inaczej inercyjny) – układ odniesienia, względem którego każde ciało, niepodlegające zewnętrznemu oddziaływaniu z innymi ciałami, porusza się bez przyspieszenia (tzn. ruchem jednostajnym prostoliniowym) lub pozostaje w spoczynku. Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona. Zgodnie z zasadą względności Galileusza wszystkie inercjalne układy odniesienia są równouprawnione i wszystkie prawa mechaniki i fizyki są w nich identyczne.

Inercjalny układ odniesienia można również zdefiniować jako taki układ, w którym nie pojawiają się pozorne siły bezwładności.

Układ nieinercjalny – układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.

Transformacja równań ruchu z układu inercjalnego do układu nieinercjalnego powoduje, że w równaniu ruchu, zapisanym w układzie nieinercjalnym, pojawiają się dodatkowe wyrazy, których wartość zależy od ruchu układu nieinercjalnego względem inercjalnego. Wyrazy te mają wymiar siły i dlatego mówimy, że w takim układzie występują pozorne siły. Nazywane są one siłami bezwładności i należą do nich, np. siła odśrodkowa i siła Coriolisa.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
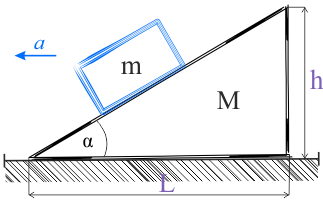
- masa klina \(M=3\,\mathrm{kg}\),
- masa klocka \(m=2\,\mathrm{kg}\),
- wysokość klina \(h=1\,\mathrm{m}\),
- długość podstawy klina \(L=2\,\mathrm{m}\),
- współczynnik tarcia między klinem a klockiem \(\mu=0,2\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- możliwe wartości przyspieszenia klina \(a\).

Analiza sytuacji

W nieinercjalnym układzie odniesienia, związanym z poruszającym się klinem, na klocek działają siły:

  • siła ciężkości klocka – w dół, siła reakcji \(R\) nachylonej powierzchni klina, prostopadła do powierzchni, skierowana w górę,
  • siła tarcia statycznego \(T\), działająca równolegle do nachylonej powierzchni klina,
  • siła bezwładności o wartości \(F_b=ma\), gdzie \(a\) jest przyspieszeniem klina.

Siła bezwładności działa przeciwnie do przyspieszenia klina względem stołu. Zgodnie z warunkami zadania, klocek nie powinien przesuwać się względem klina, czyli zgodnie z I zasadą dynamiki siły te powinny się równoważyć. Uwaga: W zależności od przyspieszenia klina siła tarcia może działać w kierunku:

  1. w dół nachylonej powierzchni klina – dla małych wartości przyspieszeń,
  2. w górę nachylonej powierzchni klina – dla dużych wartości przyspieszeń.

Rysunek

Opis rysunku

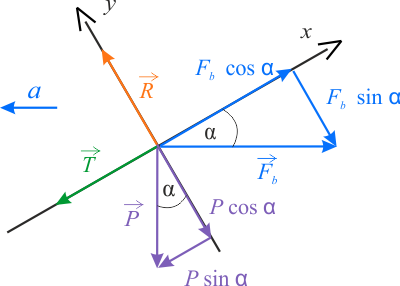
1. Siła tarcia działa w dół.

Na rysunku obok przedstawiono diagram sił działających na klocek, w układzie współrzędnych \(x\), \(y\), przy czym oś \(x\)  jest skierowana równolegle do powierzchni klina w górę, a oś \(y\) jest do niej prostopadła i skierowana w górę. Siły są reprezentowane one przez ich wartości bezwzględne.

Opis matematyczny

Warunki równowagi sił działających na klocek w tym układzie mają postać:

\(\begin{eqnarray} \begin{cases} \sum F_x &=ma\cos \alpha -mg\sin\alpha -T=0\\ \sum F_y &=R-mg\cos \alpha -ma\sin\alpha=0 \end{cases} \end{eqnarray} \),

przy czym założyliśmy, że siła tarcia działa w dół. Z pierwszego równania widzimy, że siła tarcia statycznego równoważy, w tym przypadku, wypadkową sił \(ma\cos \alpha\) i \(mg\sin \alpha\). Ale ma to miejsce tylko dla maksymalnej wartości siły tarcia statycznego \(T_{max}= \mu\,N\), gdzie \(N\) jest siłą nacisku klocka na powierzchnię klina. Siła ta jest równa co do wartości, zgodnie z III zasadą dynamiki, sile reakcji \(R\), która z kolei, zgodnie z drugim równaniem, jest równa \(mg\cos \alpha -ma\sin\alpha\). Tak więc

\(T_{max}=\mu m(g\cos \alpha +a\sin\alpha)\)

Wiemy, że \(T=\mu R\). Po podstawieniu wartości zapisanych w równaniu powyżej, mamy:

\(m(a\cos \alpha-g\sin \alpha)=\mu m(g\cos\alpha +a\sin \alpha)\)
 \[a\cos \alpha-g\sin \alpha=\mu g\cos\alpha +\mu a\sin \alpha\] \[a\cos \alpha-a\mu\sin \alpha=g\sin\alpha +\mu g\cos\alpha\] \[\displaystyle{a=\frac{\mu g\cos\alpha +g\sin \alpha}{\cos\alpha-\mu\sin\alpha} }\] 
\(\displaystyle{a=\frac{g(\mu\cos\alpha +\sin \alpha)}{\cos\alpha-\mu\sin\alpha} }\)
\(\displaystyle{a=7,8\,\mathrm{\frac{m}{s^2}} }\)

To przyspieszenie jest maksymalnym przyspieszeniem, przy którym klocek jest w spoczynku, dla większego klocek zacznie poruszać się w górę klina.

Na podstawie danych wymiarów równi wiemy, że \(\displaystyle{\operatorname{tg}{\alpha}=\frac{h}{L} }\). Otrzymane powyżej równanie \(\displaystyle{a=\frac{g(\mu\cos\alpha +\sin \alpha)}{\cos\alpha-\mu\sin\alpha} }\), należy tak przekształcić, aby wykorzystać funkcje tangens.

\(\displaystyle{a=g\,\frac{\frac{1}{\cos\alpha}(\mu\cos\alpha +\sin \alpha)}{\frac{1}{\cos\alpha}(\cos\alpha-\mu\sin\alpha)} }\)
 \[\displaystyle{a=g\,\frac{\mu +\operatorname{tg}{\alpha} }{1-\mu \operatorname{tg}{\alpha}} }\] \[\displaystyle{a=g\,\frac{\mu +\frac{h}{L} }{1-\mu \frac{h}{L}} }\] \[\displaystyle{a=g\cdot \frac{L\mu+h}{L}\cdot \frac{L}{L-\mu h} }\] 
\(\displaystyle{a=g\cdot \frac{L\mu+h}{L-\mu h} }\)

\(\displaystyle{a=10\cdot \frac{2\cdot 0,2+1}{2-0,2\cdot 1}=7,8\,\mathrm{\frac{m}{s^2}} }\)
Rysunek

Opis rysunku

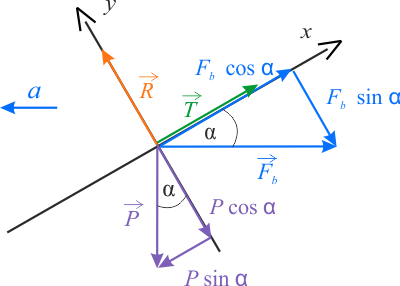
2. Siła tarcia działa w górę.

Na rysunku obok przedstawiono diagram sił działających na klocek, gdzie założyliśmy, że siła tarcia działa w górę. To znaczy, że rozpatrujmy teraz sytuację, gdy przyspieszenie klina, a co za tym idzie siła bezwładności, jest tak mała, że siła tarcia musi przeciwdziałać temu, aby klocek nie zsunął się z klina.

Opis matematyczny

Warunki równowagi sił działających na klocek w tym układzie mają postać:

\(\begin{eqnarray} \begin{cases} \sum F_x &=ma\cos \alpha -mg\sin\alpha +T=0\\ \sum F_y &=R-mg\cos \alpha -ma\sin\alpha=0 \end{cases} \end{eqnarray} \),

Z pierwszego równania widzimy, że siła tarcia statycznego równoważy, w tym przypadku wypadkową sił \(mg\sin \alpha\) i \(ma\cos \alpha\). Ma to miejsce znowu tylko do maksymalnej wartości siły tarcia statycznego \(T_{max}=\mu m(g\cos \alpha +a\sin\alpha)\). Podstawiając wartość \(T_{max}\) do pierwszego równania znajdujemy, odpowiadające tej krytycznej wartości siły tarcia statycznego, przyspieszenie:

 Podstawiając do zależności \(T=\mu R\) otrzymane równania mamy:\[g\sin\alpha-a\cos\alpha=\mu g\cos\alpha+\mu a\sin\alpha\]\[g\sin\alpha-\mu g\cos\alpha=\mu a\sin\alpha+a\cos\alpha\] 
\(\displaystyle{a=\frac{g(\sin \alpha -\mu\cos\alpha)}{\cos\alpha+\mu\sin\alpha} }\)
 \[\displaystyle{a=g\frac{\frac{1}{\cos\alpha}(\sin \alpha -\mu\cos\alpha)}{\frac{1}{\cos\alpha}(\cos\alpha+\mu\sin\alpha)} }\] \[\displaystyle{a=\frac{\operatorname{tg}{\alpha}-\mu}{\mu\operatorname{tg}{\alpha}+1} }\] \[\displaystyle{a=\frac{\frac{h}{L}-\mu}{\mu\frac{h}{L}+1} }\] \[\displaystyle{a=\frac{0,5-0,2}{0,2\cdot 0,5+1}=2,7 }\] 
\(\displaystyle{a=2,7\,\mathrm{\frac{m}{s^2}} }\)

To przyspieszenie jest minimalnym przyspieszeniem, przy którym klocek jest w spoczynku, dla większego klocek zacznie poruszać się w górę klina.

Ostatecznie znajdujemy zakres wartości przyspieszeń przyspieszenia klina, dla których klocek jest względem niego nieruchomy:

\(\displaystyle{a\in \left [ 2,7\frac{m}{s^2},\,7,8\frac{m}{s^2}\right ] }\)

Odpowiedź

Zakres wartości przyspieszeń przyspieszenia klina, dla których klocek jest względem niego nieruchomy wynosi \(\displaystyle{a\in \left [ 2,7\frac{m}{s^2},\,7,8\frac{m}{s^2}\right ]}\).