Zadanie 3.6.1.3
Ruch po okręgu w płaszczyźnie pionowej
Kulka o masie \(0,1\,\mathrm{kg}\), przywiązana do nici o długości \(50\,\mathrm{cm}\), porusza się w płaszczyźnie pionowej ze stałą prędkością liniową \(\displaystyle{2,5\,\mathrm{\frac{m}{s}} }\). Ile wynosi, w najwyższym i w najniższym punkcie toru, siła naprężenia nici? Zadanie rozwiąż w układzie inercjalnym i nieinercjalnym związanym z Ziemią.
Wskazówka teoretyczna
Teoria - układ inercjalny i nieinercjalny
Układ inercjalny (inaczej inercyjny) – układ odniesienia, względem którego każde ciało, niepodlegające zewnętrznemu oddziaływaniu z innymi ciałami, porusza się bez przyspieszenia (tzn. ruchem jednostajnym prostoliniowym) lub pozostaje w spoczynku. Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona. Zgodnie z zasadą względności Galileusza wszystkie inercjalne układy odniesienia są równouprawnione i wszystkie prawa mechaniki i fizyki są w nich identyczne.
Inercjalny układ odniesienia można również zdefiniować jako taki układ, w którym nie pojawiają się pozorne siły bezwładności.
Układ nieinercjalny – układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.
Transformacja równań ruchu z układu inercjalnego do układu nieinercjalnego powoduje, że w równaniu ruchu, zapisanym w układzie nieinercjalnym, pojawiają się dodatkowe wyrazy, których wartość zależy od ruchu układu nieinercjalnego względem inercjalnego. Wyrazy te mają wymiar siły i dlatego mówimy, że w takim układzie występują pozorne siły. Nazywane są one siłami bezwładności i należą do nich, np. siła odśrodkowa i siła Coriolisa.
Inercjalny układ odniesienia można również zdefiniować jako taki układ, w którym nie pojawiają się pozorne siły bezwładności.
Układ nieinercjalny – układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.
Transformacja równań ruchu z układu inercjalnego do układu nieinercjalnego powoduje, że w równaniu ruchu, zapisanym w układzie nieinercjalnym, pojawiają się dodatkowe wyrazy, których wartość zależy od ruchu układu nieinercjalnego względem inercjalnego. Wyrazy te mają wymiar siły i dlatego mówimy, że w takim układzie występują pozorne siły. Nazywane są one siłami bezwładności i należą do nich, np. siła odśrodkowa i siła Coriolisa.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa kulki \(m=0,1\,\mathrm{kg}\),
- długość nici \(L=50\,\mathrm{cm}=0,5\,\mathrm{m}\),
- prędkość liniowa kulki \(\displaystyle{v=2,5\,\mathrm{\frac{m}{s}}}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- siła naprężenia nici w najwyższym punkcie toru \(F_{N1}\),
- siła naprężenia nici w najniższym punkcie toru \(F_{N2}\).
Odpowiedź
Siły naprężeń nici wynoszą:
- w najwyższym punkcie toru \(\displaystyle{F_{N1}=0,25\,\mathrm{N} }\),
- w najniższym punkcie toru \(\displaystyle{F_{N2}=2,25\,\mathrm{N} }\).
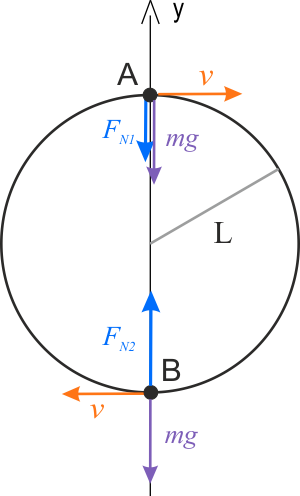
Analiza sytuacji - układ inercjalny
W układzie inercjalnym związanym z Ziemią na kulkę działają następujące siły:
- siła ciężkości \(mg\) skierowana w dół,
- siła naprężenia nici \(F_N\) skierowana w najwyższym punkcie toru w dół, a w najniższym – w górę.
Na rysunku przedstawiono tor ruchu kulki oraz jej położenia w najwyższym \(A\) i w najniższym \(B\) punkcie toru oraz diagram sił działających na kulkę w tych punktach, w jednowymiarowym układzie współrzędnych (osi \(y\) skierowana jest pionowo w górę). Siły są reprezentowane przez ich wartości bezwzględne.
Układ inercjalny.
Analiza matematyczna
Siła wypadkowa ma charakter siły dośrodkowej \(F_d\) tj. takiej, która powoduje przyspieszenie dośrodkowe.
\(\displaystyle{F_d=ma_d=m\frac{v^2}{L} }\),
gdzie długość nici jest promieniem okręgu, po którym porusza się kulka. II zasada dynamiki zapisana dla sił działających na kulkę w kierunku osi \(y\), ma postać:
- dla punktu \(A\): \(\displaystyle{-mg-F_{N1}=-m\frac{v^2}{L}}\),
- dla punktu \(B\): \(\displaystyle{F_{N2}-mg=m\frac{v^2}{L}}\).
- dla punktu \(A\): \(\displaystyle{F_{N1}=m\,(\frac{v^2}{L}-g) }\),
- dla punktu \(B\): \(\displaystyle{F_{N2}=m\,(\frac{v^2}{L}+g) }\).
\(\displaystyle{F_{N1}=0,25\,\mathrm{N} }\)
\(\displaystyle{F_{N2}=2,25\,\mathrm{N} }\)
\(\displaystyle{F_{N1}=m\,(\frac{v^2}{L}-g) }\) \(\displaystyle{F_{N2}=m\,(\frac{v^2}{L}+g) }\)
\(\displaystyle{F_{N1}=0,1\,(\frac{2,5^2}{0,5}-10) }\) \(\displaystyle{F_{N2}=0,1\,(\frac{2,5^2}{0,5}+10) }\)
\(\displaystyle{F_{N1}=0,25\,\mathrm{N}}\) \(\displaystyle{F_{N2}=2,25\,\mathrm{N} }\)
\(\displaystyle{\left [ \mathrm{kg\cdot \left (\frac{\frac{m^2}{s^2}}{m}-\frac{m}{s^2} \right )=kg\cdot\left (\frac{m}{s^2}-\frac{m}{s^2}\right )=kg\cdot \frac{m}{s^2}=N }\right ] }\)
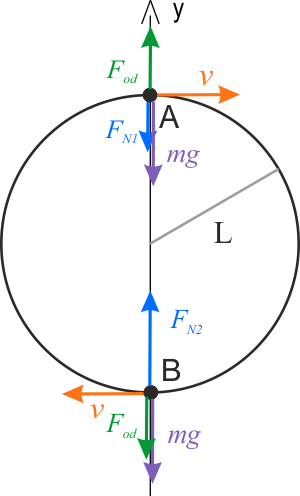
Analiza sytuacji - układ nieinercjalny
W układzie nieinercjalnym związanym z kulką (jako obserwatora nieinercjalnego wyobraźmy sobie na kuli „małego wirtualnego obserwatora”) działają następujące siły:
- siła ciężkości \(mg\) skierowana w dół,
- siła naprężenia nici \(F_N\) skierowana najwyższym punkcie toru w dół a w najniższym – w górę,
- odśrodkowa siła siłę bezwładności \(F_{od}\) skierowana w najwyższym punkcie toru w górę, a w najniższym – w dół.
Na rysunku przedstawiono tor ruchu kulki oraz jej położenia w najwyższym \(A\) i w najniższym \(B\) punkcie toru oraz diagram sił działających na kulkę w tych punktach, w jednowymiarowym układzie współrzędnych (osi \(y\) skierowana jest pionowo w górę). Siły są reprezentowane przez ich wartości bezwzględne.
Układ nieinercjalny
Analiza matematyczna
Wartość siły odśrodkowej wyraża się wzorem:
\(\displaystyle{F_{od}=m\frac{v^2}{L} }\),
Warunek równowagi sił (z I zasady dynamiki), zapisany dla kulki w położeniach \(A\) i \(B\), ma postać:
- dla punktu \(A\): \(\displaystyle{m\frac{v^2}{L}-mg-F_{N1}=0 }\),
- dla punktu \(B\): \(\displaystyle{F_{N2}-mg-m\frac{v^2}{L}=0 }\).
- dla punktu \(A\): \(\displaystyle{F_{N1}=m\,(\frac{v^2}{L}-g) }\),
- dla punktu \(B\): \(\displaystyle{F_{N2}=m\,(\frac{v^2}{L}+g) }\).
\(\displaystyle{F_{N1}=0,25\,\mathrm{N} }\)
\(\displaystyle{F_{N2}=2,25\,\mathrm{N} }\)
\(\displaystyle{F_{N1}=m\,(\frac{v^2}{L}-g) }\) \(\displaystyle{F_{N2}=m\,(\frac{v^2}{L}+g) }\)
\(\displaystyle{F_{N1}=0,1\,(\frac{2,5^2}{0,5}-10) }\) \(\displaystyle{F_{N2}=0,1\,(\frac{2,5^2}{0,5}+10) }\)
\(\displaystyle{F_{N1}=0,25\,\mathrm{N}}\) \(\displaystyle{F_{N2}=2,25\,\mathrm{N} }\)
\(\displaystyle{\left [ \mathrm{kg\cdot \left (\frac{\frac{m^2}{s^2}}{m}-\frac{m}{s^2} \right )=kg\cdot\left (\frac{m}{s^2}-\frac{m}{s^2}\right )=kg\cdot \frac{m}{s^2}=N }\right ] }\)