Zadanie 3.6.1.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.6. Nieinercjalne układy odniesienia
  4. 3.6.1 Nauka
  5. Zadanie 3.6.1.5

 Zadanie 3.6.1.5

Wirująca ciecz
Cylindryczne naczynie z cieczą obraca się z prędkością kątową \(\omega\) wokół pionowej osi, przechodzącej przez jego środek. Wyznacz kształt swobodnej powierzchni wirującej cieczy. Przyspieszenie ziemskie wynosi \(g\).

 Wskazówka teoretyczna

 Teoria - siła dośrodkowa i odśrodkowa
Jeśli ciało o masie \(m\) porusza się po okręgu o promieniu \(r\), tzn., że wypadkowa wszystkich sił działających na to ciało jest siłą dośrodkową. Wektor siły dośrodkowej skierowany jest w stronę środka okręgu, po którym porusza się ciało.

\(\displaystyle{F_{wyp}=F_{doś}=m\frac{v^2}{r} }\)

Siła odśrodkowa bezwładności, działająca na ciało o masie \(m\), w nieinercjalnym układzie odniesienia, wirującym z prędkością kątową wynosi:

\(\displaystyle{F_{od}=m\omega^2r=m\frac{v^2}{r} }\)

Wektor siły odśrodkowej skierowany jest w kierunku od środka okręgu, po którym porusza się ciało.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- prędkość kątowa naczynia \(\omega\),
- przyspieszenie ziemskie \(g\).

Szukane:
- kształt swobodnej powierzchni wirującej cieczy.

Analiza sytuacji

Rozważmy siły działające na element powierzchni cieczy o masie \(\Delta m\). Gdy powierzchnia cieczy przyjmuje ustalony kształt, to oczywiście oznacza, że siły te równoważą się dając siłę wypadkową równą zero. Przy tym o, tych siłach, możemy powiedzieć jeszcze więcej, wypadkowa siła zewnętrzna jak i siła reakcji cieczy są prostopadłe do powierzchni cieczy. Jeśli wypadkowa siła zewnętrzna nie będzie prostopadła do powierzchni cieczy, to ta powierzchnia ulegnie zmianie pod działaniem składowej siły stycznej do niej. Zmiana będzie zachodzić tak długo, aż składowa styczna zmaleje do zera. Wynika to stąd, że siła reakcji cieczy może być tylko prostopadła do jej powierzchni swobodnej.

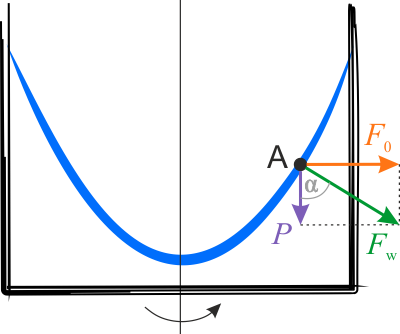
Rysunek

Na element powierzchni cieczy działa pionowo siła ciężkości o wartości \(P=\Delta mg\) oraz poziomo siła odśrodkowa bezwładności o wartości \(F_0=\Delta m \omega^2x\), gdzie \(x\) jest odległością elementu cieczy od osi obrotu.

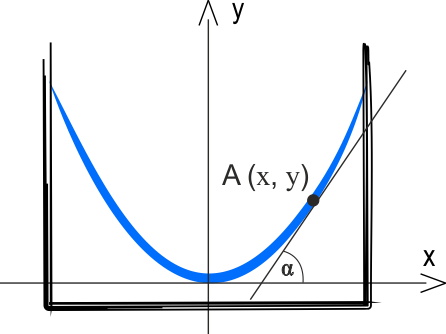
Rysunek


Na rysunku został wprowadzony układ współrzędnych po to, aby zapisać równanie \(y=y(x)\) przekroju osiowego powierzchni wirującej cieczy.

Opis matematyczny

Wyznaczmy najpierw kąt nachylenia  W matematyce styczną do krzywej w punkcie \(A\) jest prosta, będąca granicą siecznych do krzywej przechodzących przez punkty \(A\) i \(Q\), gdy \(Q\) dy do \(P\). Granica ta nie zawsze istnieje, ale jej istnienie związane jest z istnieniem pochodnej funkcji wyznaczającej tę krzywą.  do powierzchni cieczy, czyli innymi słowy, wartość pochodnej \(\displaystyle{\frac{\mathrm{d} y}{\mathrm{d} x}}\) w jakimś zadanym punkcie \(A\).  Jeżeli funkcja \(f\) jest określona w punkcie \(x_0\), to zachodzi związek \(f'(x_0)=\operatorname{tg}{\alpha} \), gdzie \(\alpha\) jest katem nachylenia do osi \(x\) stycznej do wykresu funkcji w punkcie \(P(x_0, f(x_0))\). 

\(\displaystyle{\operatorname{tg}{\alpha}=\frac{F_0}{P}=\frac{\Delta m\omega^2x}{\Delta mg} }\)
\(\displaystyle{\operatorname{tg}{\alpha}=\frac{\omega^2x}{g} }\)

Tak więc pochodna wynosi:
\(\displaystyle{\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\omega^2x}{g} }\)

Rozdzielamy zmienne
\(\displaystyle{\mathrm{d}y=\frac{\omega^2x}{g} \mathrm{d}x}\)

i następnie całkujemy
\(\displaystyle{y=\int \frac{\omega^2}{g}x\,\mathrm{d}x }\)

\(\displaystyle{y=\frac{\omega^2}{g} \int x\,\mathrm{d}x }\)

\(\displaystyle{y=\frac{\omega^2}{g}\cdot \frac{1}{2} x^2+C }\)

Stałą całkowania wyznaczymy z warunku \(y(0)=0\).  Osie układu współrzędnych zostały tak dobrane, aby w początku układu współrzędnych znajdował się wierzchołek przekroju osiowego powierzchni wirującej cieczy. 

\(\displaystyle{0=\frac{\omega^2}{g}\cdot \frac{1}{2}\cdot 0+C }\)

Z założenia tego wynika, że \(C=0\). Teraz otrzymujemy równanie:

\(\displaystyle{y=\frac{1}{2}\,\frac{\omega^2}{g}\,x^2 }\)

Otrzymane równanie opisuje parabole, więc krzywa będąca przekrojem powierzchni obracającej się cieczy ma kształt paraboloidy obrotowej.

Otrzymane równanie opisuje parabole, więc krzywa będąca przekrojem powierzchni obracającej się cieczy, ma kształt paraboloidy obrotowej.

\(\displaystyle{y=\frac{1}{2}\,\frac{\omega^2}{g}\,x^2 }\)