Zadanie 3.6.2.1
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.6. Nieinercjalne układy odniesienia
  4. 3.6.2 Trening
  5. Zadanie 3.6.2.1

 Zadanie 3.6.2.1

Ciecz w cysternie
W samochodzie cysternie jest przewożona benzyna. W pewnej chwili samochód hamuje z opóźnieniem \(\displaystyle{5\,\mathrm{\frac{m}{s^2}} }\). Ile wynosi kąt, o który poziom cieczy odchyla się od poziomu w czasie tego hamowania?

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- opóźnienie (wartość przyspieszenia) samochodu cysterny \(\displaystyle{a=5\,\mathrm{\frac{m}{s^2}} }\),
- przyspieszenie ziemskie \(\displaystyle{10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- kąt, o który poziom cieczy odchyla się od poziomu \(\alpha\).

Odpowiedź

Wartość kąta, o który poziom cieczy odchyla się od poziomu w czasie hamowania, wynosi \(\alpha=27^{\circ}\).

Polecenie

 Rozpatrzmy zachowanie się cieczy w czasie hamowania samochodu. Jako układ odniesienia wybierzmy układ związany z cysterną. Jakiego rodzaju jest to układ?

Wybór 1 z 2

Układ inercjalny

Odpowiedź nieprawidłowa

Wybór 2 z 2

Układ nieinercjalny

Odpowiedź prawidłowa
Jest to układ nieinercjalny, w którym na każdą porcję \(\Delta m\) masy benzyny działa siła bezwładności o wartości \(F_b=\Delta a\).

Polecenie

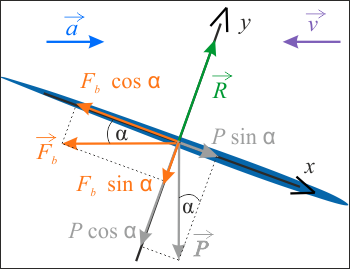
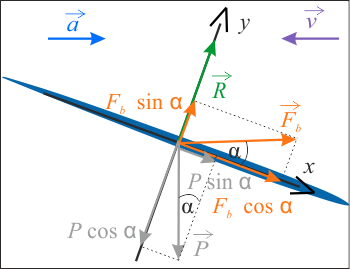
Sporządź wykres ilustrujący sytuacje z zadania. Wybierz jeden prawidłowy, wśród dwóch przedstawionych poniżej.

Wybór 1 z 2

Rysunek

Odpowiedź prawidłowa

Wybór 2 z 2

Rysunek

Odpowiedź nieprawidłowa
Błędnie wyznaczony kierunek siły bezwładności.
W układzie związanym z cysterną, na każdą masę \(\Delta m\) działają następujące siły: siła ciężkości \(P=\Delta mg\) – skierowana pionowo w dół, siła bezwładności \(F_b=\Delta ma\) – skierowana przeciwnie do wektora przyspieszenia samochodu oraz siła reakcji \(R\) cieczy (wynikająca z oddziaływań międzycząsteczkowych cząsteczek) – skierowana prostopadłe do powierzchni cieczy na zewnątrz cieczy.

Polecenie

Wyznacz kąt, o który poziom cieczy odchyla się od poziomu. Wybierz jedną prawidłową odpowiedź, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\alpha=23^{\circ}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\alpha=25^{\circ}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\alpha=27^{\circ}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(\alpha=30^{\circ}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Ponieważ ciecz nie przemieszcza się względem cysterny, to zgodnie z I zasadą dynamiki, suma sił działających na każdą porcję cieczy jest równa zero. Dla składowych w kierunku osi \(x\) sił, działających na porcję cieczy o masie \(\Delta m\), warunek równowagi sił ma postać:

\(\sum F_x=\Delta mg\sin\alpha-\Delta ma\cos\alpha=0\)

Skąd wyznaczamy kąt \(\alpha\), o który poziom cieczy odchyla się od poziomu. Po prostych  \[\Delta mg\sin\alpha=\Delta ma\cos\alpha\] \[g\sin\alpha=a\cos\alpha\] \[\displaystyle{\frac{\sin\alpha}{\cos\alpha}=\frac{a}{g} }\]  otrzymujemy.

\(\displaystyle{\operatorname{tg}{\alpha}=\frac{\Delta ma}{\Delta mg}=\frac{a}{g} }\)

\(\displaystyle{\operatorname{tg}{\alpha}=\frac{5}{10} }\)

Funkcja tangens przyjmuje wartość \(0,5\) dla kąta \(\alpha=27^{\circ}\).

Odpowiedź

Wartość kąta, o który poziom cieczy odchyla się od poziomu w czasie hamowania, wynosi \(\alpha=27^{\circ}\).