Zadanie 3.6.2.5
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- kąt nachylenia równi \(\alpha\),
- współczynnik tarcia \(\mu < \operatorname{tg}{\alpha}\),
- masa naczynia z wodą \(M\).
Szukane:
- kąt nachylenia powierzchni cieczy w naczyniu względem równi \(\beta\).
Odpowiedź
Kąt nachylenia powierzchni cieczy w naczyniu względem równi wynosi \(\beta=\operatorname{arctg}{\mu}\).
Polecenie
Pierwszy etap rozwiązania polega na wyznaczenia przyspieszenia naczynia z cieczą. Zapisz równanie, opisujące działanie sił równoległych do powierzchni równi. Wybierz jedną prawidłową zależność, spośród dwóch przedstawionych poniżej.
\(Ma=Mg\sin\alpha-\mu Mg\cos\alpha\)
\(Ma=Mg\sin\alpha+\mu Mg\cos\alpha\)
Rozwiązanie
W pierwszym etapie wyznaczmy przyspieszenie naczynia z cieczą. Rozłóżmy ciężar \(F_c\) (ciężar naczynia z cieczą równy \(Mg\) ) na dwie składowe - siłę \(F_s\), czyli siłę ściągającą równoległą do powierzchni równi i siłę \(F_n\) - siłę nacisku prostopadłą do powierzchni równi. Równolegle do równi działa jeszcze siła tarcia \(F_t=\mu F_n\), skierowana przeciwnie do kierunku ruchu.
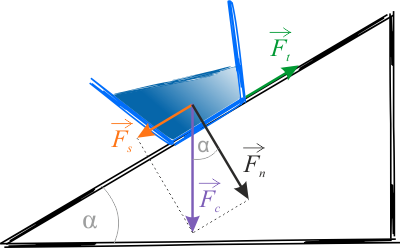
Z rysunku widać, że
Wypadkowa siły \(F_s\) i siły \(F_t\) nadaje naczyniu z cieczą o masie \(M\) przyspieszenie \(a\). Mamy więc równanie:
\(a=g\sin\alpha-\mu g\cos\alpha\)
Polecenie
Aby wyznaczyć nachylenie powierzchni cieczy w naczyniu względem równi, można związać układ odniesienia z poruszającym się naczyniem. Zapisz równanie opisujące działanie sił na cząstkę cieczy o masie \(m\). Wybierz jedną prawidłową zależność, spośród dwóch przedstawionych poniżej.
Rozwiązanie
Zwiążmy układ odniesienia z poruszającym się naczyniem. Na każdą cząsteczkę cieczy o masie \(m\), w tym układzie, działa siła ciężkości \(P=mg\) i siła bezwładności \(\vec{F}_b=-m\,\vec{a}\), gdzie znak minus oznacza, że siła ta jest przeciwnie skierowana do wektora \(\vec{a}\).
Na rysunku siły są reprezentowane przez ich wartości bezwzględne.
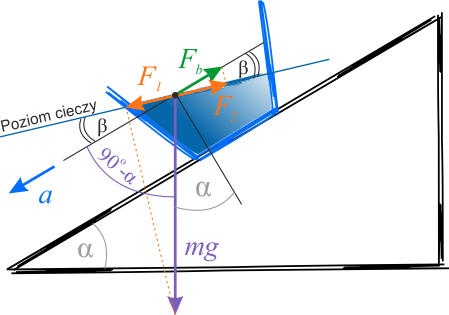
Powierzchnia cieczy ustawia się w takim położeniu, aby rzuty dwóch sił \(P\) i \(F_b\) na kierunek styczny do jej powierzchni, zrównoważyły się (czyli \(F_1=F_2\)). Jak widać z rysunku rzut siły \(F_b\) na powierzchnię cieczy wynosi:
Po przyrównaniu wartości obu rzutów otrzymujemy:
Polecenie
Wyznacz wartość kąta nachylenia powierzchni cieczy w naczyniu względem równi. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.
\(\beta=\arccos\mu\)
Rozwiązanie
Z dwóch części rozważań otrzymaliśmy zależności:
Zajmijmy się równaniem drugim. Funkcję \(\cos\,(90^{\circ}-\alpha+\beta)\) można zapisać następująco:
Stosując wzór \(\cos(90^{\circ}-\gamma)=\sin\gamma\) mamy
Rozpatrywane równanie przybiera postać:
Teraz, to tego równania, podstawiamy wartość przyspieszenia, obliczoną w pierwszej części rozwiązania
Po \[\sin\alpha\,\cos\beta-\cos\alpha\,\sin\beta=\sin\alpha\cos\beta-\mu \cos\alpha\cos\beta\] \[-\cos\alpha\,\sin\beta=-\mu \cos\alpha\cos\beta\] \[\sin\beta=\mu \cos\beta\] \[\displaystyle{\mu=\frac{\sin\beta}{\cos\beta} }\] \[\displaystyle{\mu=\operatorname{tg}{\beta} }\] otrzymujemy:
Odpowiedź
Kąt nachylenia powierzchni cieczy w naczyniu względem równi wynosi \(\beta=\operatorname{arctg}{\mu}\).
