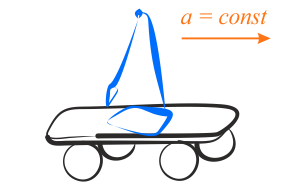Zadanie 3.6.2.4
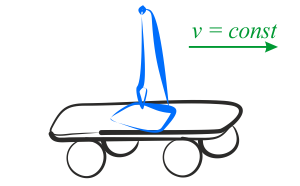
a) wózek porusza się ruchem jednostajnym po płaszczyźnie poziomej,
b) wózek porusza się po płaszczyźnie poziomej z przyspieszeniem \(a\),
c) wózek stacza się swobodnie z równi pochyłej, która tworzy kąt \(\beta\) z poziomem.
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa wahadła \(m\),
- kąt nachylenia równi \(\beta\),
- przyspieszenie ziemskie \(g\).
Szukane:
- kąt, jaki tworzy nić z pionem \(\alpha\),
- naprężenie nici \(F_N\).
Odpowiedź
Naprężenie nici oraz kąt, jaki tworzy ona z pionem, wynoszą:
a) \(F_N=mg\) oraz \(\alpha=0\),
b) \(F_N=m\sqrt{a^2+g^2}\) oraz \(\displaystyle{\alpha=\operatorname{arctg}{\frac{a}{g}} }\),
c) \(F_N=mg\cos\beta\) oraz \(\alpha=\beta\).
Polecenie
Wybierz jeden prawidłowy rysunek, spośród trzech, ilustrujący sytuację opisaną w punkcie a).
Polecenie - punkt a)
Wskaż spośród trzech zestawów ten, w którym napisano prawidłowe wartości kąta \(\alpha\) oraz siły \(F_N\) dla sytuacji, gdy wózek porusza się ruchem jednostajnym po płaszczyźnie poziomej.
\(\displaystyle{\alpha=\operatorname{arctg}{\frac{a}{g}} }\)
\(F_N=m\sqrt{a^2+g^2}\)
\(\alpha=\beta\)
\(F_N=mg\cos\beta\)
\(\alpha=0\)
\(F_N=mg\)
Rozwiązanie
W każdym z przypadków kierunek nici wahadła wyznaczony będzie przez wypadkową siłę zewnętrzną \(F_w\), działającą na wahadło. Trzeba tu dodać, że siła ta będzie zawsze równoważona przez siłę reakcji nici \(F_N\) tak, że wypadkowa siła działająca na wahadło będzie równa zeru. Widać tu, że siły opisujemy w układzie odniesienia, względem którego wahadło znajduje się w spoczynku, a więc w układzie związanym z poruszającym się wózkiem. W przypadku, gdy wózek będzie poruszać się z przyspieszeniem, nasz układ odniesienia będzie układem nieinercjalnym, a wypadkowa sił zewnętrznych będzie sumą sił ciężkości i bezwładności.
a) W tym przypadku mamy jedynie siłę ciężkości \(P=mg\), a więc \(F_N=F_w=mg\). Nić zachowuje kierunek pionowy: \(\alpha=0\)
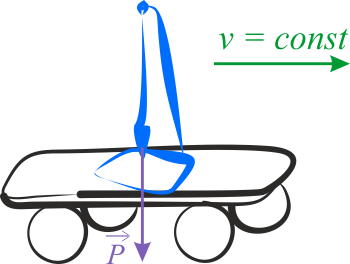
Polecenie - punkt b)
Wskaż spośród trzech zestawów ten, w którym napisano prawidłowe wartości kąta \(\alpha\) oraz siły \(F_N\) dla sytuacji, gdy wózek porusza się po płaszczyźnie poziomej z przyspieszeniem \(a\).
Rozwiązanie
W tym przypadku, oprócz siły ciężkości, na wahadło będzie działać w kierunku poziomym siła bezwładności:
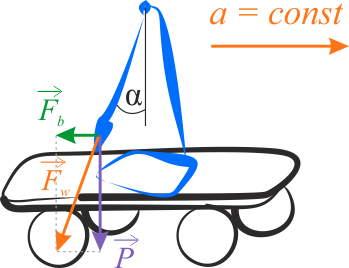
Z rysunku wynika, że
Wartość siły wypadkowej wyznaczamy następująco:
Polecenie - punkt c)
Wskaż spośród trzech zestawów ten, w którym napisano prawidłowe wartości kąta \(\alpha\) oraz siły \(F_N\) dla sytuacji, gdy wózek stacza się swobodnie z równi pochyłej, która tworzy kąt \(\beta\) z poziomem.
Rozwiązanie
W tym przypadku cały wózek będzie poruszać się w dół równi z przyspieszeniem \(a\).
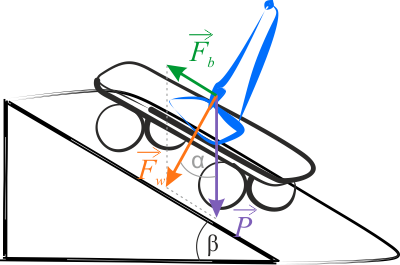
Na wahadło będzie działać siła ciężkości i bezwładności. Siła bezwładności \(F_b\) działa wzdłuż równi, w przeciwnym kierunku do przyspieszenia. Wahadło ustawi się w takim położeniu, aby rzuty tych dwóch sił na kierunek równoległy do powierzchni równi, zrównoważyły się.
Informacja
Poniżej znajduje się animacja, wyjaśniająca sposób rysowania wektorów sił działających na wahadło oraz wyjaśnienie...
Rozwiązanie
Z rysunku przedstawiającego siły działające na wahadło widać, że
Miara kąt \(\alpha\) jest taka sama jak miara kąta \(\beta\), więc mamy
Odpowiedź
Naprężenie nici oraz kąt, jaki tworzy ona z pionem, wynoszą:
a) \(F_N=mg\) oraz \(\alpha=0\),
b) \(F_N=m\sqrt{a^2+g^2}\) oraz \(\displaystyle{\alpha=\operatorname{arctg}{\frac{a}{g}} }\),
c) \(F_N=mg\cos\beta\) oraz \(\alpha=\beta\).