Zadanie 3.6.2.3
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.6. Nieinercjalne układy odniesienia
  4. 3.6.2 Trening
  5. Zadanie 3.6.2.3

 Zadanie 3.6.2.3

Samochód na zakręcie
Jaka powinna być minimalna wartość współczynnika tarcia statycznego między oponami samochodu a asfaltem, aby samochód mógł przejechać bez poślizgu, po płaskiej drodze, zakręt o promieniu \(50\,\mathrm{m}\) z prędkością \(\displaystyle{72\,\mathrm{\frac{km}{h}} }\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- promień zakrętu \(r=50\,\mathrm{m}\),
- prędkość samochodu \(\displaystyle{v=72\,\mathrm{\frac{km}{h}}=20\,\mathrm{\frac{m}{s}} }\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- współczynnik tarcia statycznego \(\mu\).

Odpowiedź

Minimalna wartość współczynnika tarcia statycznego między oponami samochodu a asfaltem wynosi \(\mu=0,8\).

Polecenie

Zastanów się, jakie siły działają na samochód znajdujący się na zakręcie. Ile sił działa na samochód w kierunku poziomym? Wybierz jedną odpowiedź, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

Jedna siła.

Odpowiedź nieprawidłowa

Wybór 2 z 4

Dwie siły.

Odpowiedź prawidłowa

Wybór 3 z 4

Trzy siły.

Odpowiedź nieprawidłowa

Wybór 4 z 4

Cztery siły.

Odpowiedź nieprawidłowa

Rysunek

Rysunek


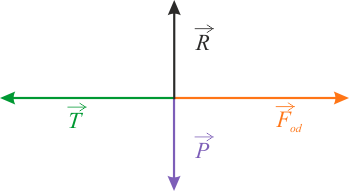
Na rysunku przedstawiono diagram sił działających na samochód w nieinercjalnym układzie odniesienia, związanym z samochodem. Wprowadzono układ współrzędnych \(x\;y\), przy czym oś \(x\) jest skierowana równolegle do jezdni na zewnątrz zakrętu, a oś \(y\) jest do niej prostopadła i skierowana w górę.

Polecenie

Oblicz ile wynosi minimalna wartość współczynnika tarcia statycznego między oponami samochodu a asfaltem, aby samochód mógł przejechać bez poślizgu, po płaskiej drodze? Wybierz jedną prawidłową odpowiedź, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\mu=0,2\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\mu=0,4\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\mu=0,6\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\mu=0,8\)

Odpowiedź prawidłowa

Rozwiązanie

Z punktu widzenia obserwatora w tym układzie nieinercjalnym, samochód jest w spoczynku, zatem zgodnie z I zasadą dynamiki, wypadkowa sił działających na samochód jest równa zeru.
Warunki równowagi dla obu osi maja postać:

\(\begin{eqnarray} \begin{cases} \sum F_x &=F_{od}-T=0 \\ \sum F_y &=R-mg=0 \end{cases} \end{eqnarray} \),

przy czym wartość odśrodkowej siły bezwładności wynosi \(\displaystyle{F_{od}=\frac{mv^2}{r}}\). Maksymalna wartość siły tarcia, przeciwdziałająca „wyrzuceniu” samochodu na zewnątrz zakrętu, wynosi \(T_{max}=\mu N\), gdzie \(N\) jest siłą nacisku samochodu na powierzchnię jezdni. Siła ta jest równa, co do wartości, zgodnie z III zasadą dynamiki, sile reakcji powierzchni jezdni \(R\), która z kolei, zgodnie z drugim równaniem, jest równa sile ciężkości \(mg\). Podstawiając do pierwszego równania wyrażenie na wartość siły odśrodkowej i \(T=T_{max}\) otrzymujemy:

\(\displaystyle{\frac{mv^2}{r}-\mu mg=0 }\)

\(\displaystyle{\frac{mv^2}{r}=\mu mg }\)

\(\displaystyle{\mu=\frac{v^2}{rg} }\)

\(\displaystyle{\mu=\frac{20^2}{10\cdot 50} }\)

\(\mu=0,8\)

Odpowiedź

Minimalna wartość współczynnika tarcia statycznego między oponami samochodu a asfaltem wynosi \(\mu=0,8\).