Zadanie 4.1.1.1
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.1. Praca sił. Energia mechaniczna
  4. 4.1.1 Nauka
  5. Zadanie 4.1.1.1

 Zadanie 4.1.1.1

Praca przy przesuwaniu ciała
Biurko o masie \(15\,\mathrm{kg}\) jest przesuwane po poziomej powierzchni pod działaniem siły zewnętrznej o wartości \(70\,\mathrm{N}\) i skierowanej pod kątem \(30^{\circ}\) do poziomu. Biurko przesunięto o \(5\,\mathrm{m}\). Współczynnik tarcia biurka o podłoże wynosi \(0,2\). Obliczyć pracę:
a) siły zewnętrznej,
b) siły ciężkości,
c) siły tarcia,
d) siły wypadkowej.

 Wskazówka teoretyczna

 Teoria - praca stałej siły
Praca \(W\) stałej siły \(F\), działającej równolegle do kierunku przesuwania się ciała, równa jest

\(W=F\,S\),

gdzie \(S\) jest długością odcinka, o jaki ciało przesunięto.

Jeśli siła \(F\) tworzy z kierunkiem przesunięcia kąt \(\alpha\), to

\(W=F_sS=F\,S\,\cos\alpha\),

gdzie \(F_s\) jest składową siły równoległą do przesunięcia (styczna do toru).

Praca nie musi być wielkością dodatnią. Dla stałej siły, gdy kąt \(\alpha\) między przesunięciem a kierunkiem działania siły wynosi \(90^{\circ}\), praca zeruje się, natomiast, gdy \(\alpha>90^{\circ}\), to praca ma wartość ujemną.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa biurka \(m=15\,\mathrm{kg}\),
- siła wykonująca pracę \(F=70\,\mathrm{N}\),
- kąt nachylenia wektora siły do poziomu \(\alpha=30^{\circ}\),
- wartość współczynnika tarcia \(\mu=0,2\),
- droga przebyta przez biurko \(S=5\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- praca wykonana przez siłę zewnętrzną \(W_F\),
- praca wykonana przez siłę ciężkości \(W_P\),
- praca wykonana przez siłę tarcia \(W_T\),
- praca wykonana przez siłę wypadkową \(W\).

Analiza sytuacji

Na biurko działają siły: siła zewnętrzna \(F\) opisana w treści zadania, siła ciężkości \(P=mg\) w dół oraz siła tarcia \(T\) przeciwnie do kierunku ruchu. Wszystkie działające na ciało siły są stałe, dlatego do rozwiązania zadania skorzystamy z definicji pracy stałej siły. Zgodnie z definicją, praca stałej siły o wartości \(F\) na drodze \(S\) wyraża się wzorem:

\(W=F\,S\,\cos\alpha\),

gdzie \(\alpha\) jest kątem między kierunkiem przesunięcia a kierunkiem działającej siły.

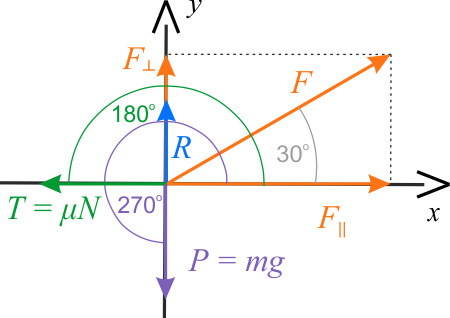
Rysunek

Opis rysunku

Na rysunku przedstawiono diagram sił działających na biurko w dwuwymiarowym układzie współrzędnych \(x\;y\), gdzie oś \(x\) skierowana jest poziomo, a oś \(y\) - w górę. Na diagramie siły reprezentowane są przez ich wartości bezwzględne.
W naszym przypadku wartość wykonanej pracy jest zależna od wartości kąta, jaki tworzy poszczególna siła z kierunkiem osi \(x\). Dla siły \(F\) wartość kąta wynosi \(30^{\circ}\), dla siły \(P\) kąt ma miarę \(270^{\circ}\), a dla siły \(T\) kąt wynosi \(180^{\circ}\) (siła tarcia działa przeciwnie do kierunku ruchu). Siła wypadkowa działa wzdłuż osi \(x\), czyli wartość kąta nachylenia siły do osi \(x\) wynosi \(0^{\circ}\).

Rozwiązanie

Przy obliczaniu pracy siły tarcia potrzebna jest wartość tej siły, która wynosi \(T=\mu N\), gdzie \(N\) – siła nacisku biurka na podłoże. Zgodnie z III zasadą dynamiki, siła ta jest równa sile reakcji podłoża \(R\), którą otrzymujemy z warunkiem równowagi sił działających wzdłuż osi \(y\).

\(\sum F_y=R+F_{\perp}-P=0\)
Stąd mamy, że
\(N=R=P-F_{\perp}=mg-F\sin\alpha\)

Przy obliczaniu pracy siły tarcia potrzebna jest wartość tej siły, która jest wypadkową działających sił wzdłuż osi \(x\) i wynosi

\(F_w=\sum F_x=F_{\parallel}-T=F\cos\alpha-\mu(mg-F\sin\alpha)\)

a) Zgodnie z definicją praca siły \(F\) (danej w zdaniu) wynosi:

\(W_F=F\cdot S\cdot\cos 30^{\circ}\)

\(W_F=70\cdot 5\cdot 0,866=303\,\mathrm{J}\)

b) Praca siły ciężkości wynosi:

\(W_P=mg\cdot S\cdot \cos 90^{\circ}\)

\(W_P=15\cdot 10\cdot 5\cdot 0=0\,\mathrm{J}\)

c) Praca siły tarcia wynosi:

\(W_T=\mu N\cdot S\cdot \cos 180^{\circ}\)

Za siłę \(N\) podstawiamy wyżej wyprowadzoną zależność i otrzymujemy:

\(W_T=\mu (mg-F\sin 30^{\circ})\cdot S\cos 180^{\circ}\)

\(W_T=0,2\cdot (15\cdot 10-70\cdot 0,5)\cdot 5\cdot (-1)=-115\,\mathrm{J}\)

d) Praca siły wypadkowej:

\(W=F_W\cdot S\cdot \cos 0^{\circ}\)

\(W=(F\cos 30^{\circ}-\mu\cdot (mg-F\sin 30^{\circ}))\cdot S\cdot \cos 0^{\circ}\)

\(W=(70\cdot 0,866-0,2\cdot (15\cdot 10-70\cdot 0,5))\cdot 5\cdot 1\)

\(W=188\,\mathrm{J}\)

 Oczywiście pracę siły wypadkowej możemy znaleźć również, jako sumę prac poszczególnych sił działających na blok. Sprawdźmy: \[W=W_F+W_P+W_T\] \[W=303+0-115=188\,\mathrm{J}\] 

Odpowiedź

Wartości poszczególnych prac wynoszą:
a) praca siły zewnętrznej \(W_F=303\,\mathrm{J}\),
b) praca siły ciężkości \(W_P=0\,\mathrm{J}\),
c) praca siły tarcia \(W_T=-115\,\mathrm{J}\),
d) praca siły wypadkowej \(W=188\,\mathrm{J}\).