Zadanie 4.1.1.2
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.1. Praca sił. Energia mechaniczna
  4. 4.1.1 Nauka
  5. Zadanie 4.1.1.2

 Zadanie 4.1.1.2

Przesuwanie deski po różnych powierzchniach
Deska o masie \(2\,\mathrm{kg}\) i długości \(L=1\,\mathrm{m}\) leży na granicy zetknięcia dwóch stołów. W chwili początkowej leży ona całą swoją długością na pierwszym z nich. Jaką minimalną pracę należy wykonać, aby przesunąć ją z jednego stołu na drugi, jeżeli współczynniki tarcia pomiędzy deską a pierwszym stołem wynosi \(0,2\), a między drugim stołem a deską \(0,4\). Przyjmij, że stoły się stykają. Rozwiąż zadanie graficznie korzystając z graficznej metody liczenia pracy sił zależnych od położenia.

 Wskazówka teoretyczna

 Teoria - praca stałej siły
Praca \(W\) stałej siły \(F\), działającej równolegle do kierunku przesuwania się ciała, równa jest

\(W=F\,S\),

gdzie \(S\) jest długością odcinka, o jaki ciało przesunięto.

Wzór na pracę ma prostą geometryczną interpretację. Mianowicie, na wykresie siły w zależności od przemieszczenia, miarą pracy jest pole powierzchni między krzywą siły a osią przemieszczeń.

Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa deski \(m=2\,\mathrm{kg}\),
- długość deski \(L=1\,\mathrm{m}\),
- współczynnik tarcia pomiędzy deską i pierwszym stołem \(\mu_1=0,2\),
- współczynnik tarcia pomiędzy deską i drugim stołem \(\mu_2=0,4\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- minimalna praca, jaką należy wykonać, aby przesunąć deskę z jednego stołu na drugi \(W_m\).

Analiza sytuacji

W treści zadania występuje określenie „minimalna praca, jaką należy wykonać”. Należy przez to rozumieć pracę siły zewnętrznej, jaka musi zostać wykonana, aby pokonać siły tarcia. Praca nie ma być zużyta na zwiększenie prędkości deski.

Innymi słowy, zgodnie z poleceniem danym w treści zadania, pracę mamy znaleźć metodą graficzną. W tej metodzie miarą pracy siły jest pole powierzchni pod krzywą zależności siły od położenia ciała.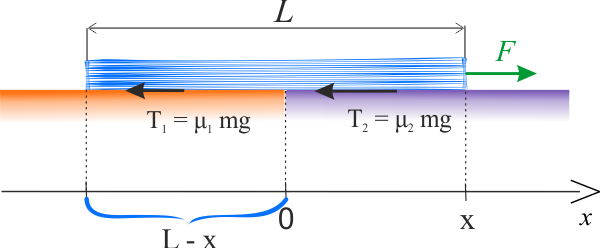

Rysunek


Na powyższym rysunku, w jednowymiarowym układzie współrzędnych osi \(x\) skierowanej w prawo, przedstawiono diagram sił działających na deskę. Wartość \(x=0\) na osi \(x\) przyjęto w punkcie złączenia stołów, siły są reprezentowane przez ich wartości bezwzględne, a wartość siły zewnętrznej oznaczyliśmy przez\(F\). Zewnętrzna siła równoważy sumę siły tarcia: \(T_1\) – deski o powierzchnię pierwszego stołu i \(T_2\) – deski o powierzchnię drugiego stołu.

Przyjmijmy, że część deski o długości \(x\) leży na drugim stole, wówczas wartość siły zewnętrznej można zapisać jako:
\(F=T_1+T_2\)

\(\displaystyle{T_1=\mu_1\,mg \frac{L-x}{L}}\)

\(\displaystyle{T_2=\mu_2\,mg \frac{x}{L}}\)

\(\displaystyle{F=\mu_1\,mg \frac{L-x}{L}+\mu_2\,mg \frac{x}{L}}\)
Po  \[\displaystyle{F=\mu_1\,mg\left (\frac{L}{L}-\frac{x}{L}\right )+\mu_2\,mg \frac{x}{L}}\] \[\displaystyle{F=\mu_1\,mg\frac{L}{L}-\mu_1\,mg\frac{x}{L}+\mu_2\,mg \frac{x}{L}}\]  otrzymujemy
\(\displaystyle{F=\mu_1\,mg +(\mu_2-\mu_1)\,mg \frac{1}{L}\cdot x }\)

Wykres

Zależność, opisująca siłę zewnętrzną, ma postać prostej \(F(x)=A-Bx\), gdzie

\(A=\mu_1\,mg \)    oraz     \(\displaystyle{B=(\mu_2-\mu_1)\,mg \frac{1}{L}}\)

Wynika stąd, że siła zmienia się liniowo.
Wartość początkową i końcową wyznaczymy odpowiednio dla \(x=0\) oraz dla \(x=L\).

\(F(0)=\mu_1\,mg\)

\(\displaystyle{F(L)=\mu_1\,mg+(\mu_2-\mu_1)\,mg \frac{L}{L} }\)

\(F(L)=\mu_1\,mg+\mu_2mg-\mu_1mg \)

\(F(L)=\mu_2mg\)

Na podstawie przeprowadzonej analizy możemy narysować wykres, przedstawiający pracę wykonaną przez siłę \(F\).

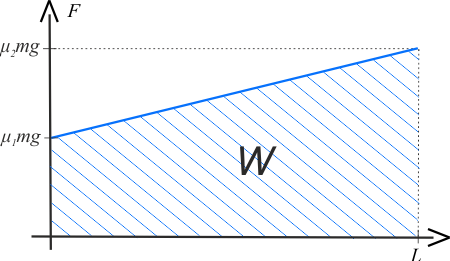
Wykres


Wartość pracy, wykonanej przez siłę \(F\), jest równa zakreskowanemu polu powierzchni pod prostą \(F(x)\).

Zgodnie z rysunkiem praca \(W\) wykonanej przez siłę \(F\), jest równa, co do wartości, polu trapezu lub polu prostokąta \(+\) trójkąta.

Rozwiązanie - trapez
Rysunek


Pole trapezu wynosi:
\(\displaystyle{W=\frac{1}{2} (\mu_1\,mg+\mu_2\,mg)\,L }\)

\(W=0,5\cdot (0,2+0,4)\cdot 2 \cdot 10\cdot 1\)

\(W=6\,\mathrm{J}\)
Rozwiązanie - trójkąt i prostokąt
Rysunek

Pole pod wykresem, rozdzielone na trójkąt i prostokąt, obliczamy następująco:

\(W=P_T+P_P\)

\(W=0,5\cdot L(\mu_2\,mg-\mu_1\,mg)+\mu_1\,mg\cdot L\)

\(W=0,5L\,\mu_2\,mg+0,5L\,\mu_1\,mg\)

\(W=0,5L\,mg(\mu_2+\mu_1)\)

\(W=0,5\cdot 1\cdot 2\cdot 10\,(0,4+0,2)\)

\(W=6\,\mathrm{J}\)

  1. Oczywiście możemy obliczyć pracę z definicji \(\displaystyle{W=\int_{0}^{L}F\,\mathrm{d}x}\), gdzie za \(F\) podstawiamy otrzymaną wcześniej zależność.
  2. Praca wykonana przez siły tarcia, jest równa, co do wartości bezwzględnej, pracy siły \(F\). Wartość ta jest ujemna.

Odpowiedź

Wartość minimalnej pracy, jaką należy wykonać, aby przesunąć deskę z jednego stołu na drugi, wynosi \(W=6\,\mathrm{J}\).