Zadanie 4.1.1.3
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.1. Praca sił. Energia mechaniczna
  4. 4.1.1 Nauka
  5. Zadanie 4.1.1.3

 Zadanie 4.1.1.3

Wjazd pod górkę pojazdu o zadanej mocy silnika
Z jaką największą stałą prędkością może wjeżdżać samochód o masie \(1000\,\mathrm{kg}\) po wzniesieniu o nachyleniu \(30^{\circ}\), jeżeli maksymalna moc silnika wynosi \(50\,\mathrm{kW}\)? Przyjmij, że efektywny współczynnik tarcia wynosi \(0,1\), a opór powietrza można pominąć.

 Wskazówka teoretyczna

 Teoria - moc
Moc \(P\) - skalarna wielkość fizyczna określająca pracę \(W\) wykonaną przez układ fizyczny w jednostce czasu \(t\). Moc jest równa również iloczynowi skalarnemu wektorów: siły i prędkości.

\(\displaystyle{P=\frac{\mathrm{d}W }{\mathrm{d} t}=\vec{F}\,\vec{v}}\)

Jeżeli praca wykonywana jest w stałym tempie, to mamy

\(\displaystyle{P=\frac{W}{t}}\)

W przeciwnym wypadku powyższy wzór będzie określał moc średnią.

\(\displaystyle{P_{śr}=\frac{W}{t}}\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa samochodu \(m=1000\,\mathrm{kg}\),
- kąt nachylenia wzgórza do poziomu \(\alpha=30^{\circ}\),
- wartość współczynnika tarcia \(\mu =0,1\),
- maksymalna moc silnika samochodu \(P_{max}=50\,\mathrm{kW}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- największa możliwa stała prędkość samochodu \(v_{max}\).

Analiza sytuacji

Na samochód jadący po wzniesieniu działają następujące siły:

  • siła napędowa silnika \(F\) pod górę, równolegle pod wzniesienie;
  • siła ciężkości \(mg\) pionowo w dół;
  • siła reakcji podłoża \(R\) prostopadle do podłoża w górę;
  • siła tarcia \(T\) równolegle do wzniesienia i przeciwnie do kierunku ruchu.
Ponieważ samochód jedzie ze stałą prędkością, to siła ciągu silnika równoważy sumę sił działających przeciwne do kierunku ruchu samochodu.

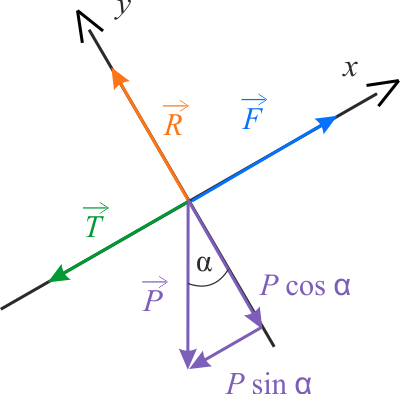
Rysunek


Powyżej przedstawiono diagram sił działających na samochód w dwuwymiarowym układzie współrzędnych \(x\,y\), gdzie oś \(x\) jest skierowana równolegle do wzniesienia, w stronę wierzchołka, a oś \(y\) skierowana jest prostopadle do niej, w górę. Ponieważ samochód porusza się ze stałą prędkością, muszą być spełnione warunki równowagi dla kierunków \(x\) i \(y\):

\(\begin{eqnarray} \begin{cases} \sum F_x &= F-mg\sin\alpha-T=0\\ \sum F_y &=R-mg\cos\alpha=0 \end{cases} \end{eqnarray} \)

Siła tarcia ma wartość \(T =\mu N\), gdzie \(N\) – siła nacisku samochodu na podłoże. Zgodnie z III zasadą dynamiki, siła ta jest równa sile reakcji podłoża \(R\), a zgodnie z warunkiem równowagi sił wzdłuż osi \(y\) mamy:

\(R=mg\cos\alpha\)

Wracając do pierwszego równania otrzymujemy, że siła napędowa silnika wynosi:

\(F=mg\sin\alpha+\mu mg\cos\alpha\)

Związek między mocą silnika a siłą napędową pozwala określić zależność:

\(\displaystyle{P=\frac{W}{t}=\frac{F\cdot S}{t}=F\cdot v }\)

Rozwiązanie

Z poprzednio wyprowadzonych równań otrzymaliśmy

\(P=F\cdot v\)
Maksymalna wartość prędkości będzie więc wynosić

\(\displaystyle{v_{max}=\frac{P_{max}}{F} }\)

\(\displaystyle{v_{max}=\frac{P_{max}}{mg\cdot (\sin\alpha+\mu\cdot \cos\alpha)} }\)

\(\displaystyle{v_{max}=\frac{50\cdot 10^3}{1000\cdot 10\cdot (\sin 30^{\circ}+0,1\cdot \cos30^{\circ})} }\)

\(\displaystyle{v_{max}=8,52\,\mathrm{\frac{m}{s}}=30,7\,\mathrm{\frac{km}{h}} }\)
 \[\frac{W}{kg\cdot\frac{m}{s^2}}=W\cdot\frac{s^2}{kg\cdot m}=\frac{J}{s}\cdot\frac{s^2}{kg\cdot m}=\] \[=J\cdot\frac{s}{kg\cdot m}=N\cdot m\cdot\frac{s}{kg\cdot m}=N\cdot\frac{s}{kg}=\] \[=\frac{m}{s^2}\cdot kg\cdot\frac{s}{kg}=\frac{m}{s}\] 

Odpowiedź

Samochód ten może wjeżdżać na wzniesienie z maksymalną stałą prędkością, wynoszącą \(\displaystyle{v_{max}=8,52\,\mathrm{\frac{m}{s}}=30,7\,\mathrm{\frac{km}{h}} }\).