Zadanie 4.1.1.4
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.1. Praca sił. Energia mechaniczna
  4. 4.1.1 Nauka
  5. Zadanie 4.1.1.4

 Zadanie 4.1.1.4

Praca siły tarcia

Klocek o masie \(0,5\,\mathrm{kg}\) przesuwany jest po podłodze. Współczynnik tarcia kinetycznego między klockiem a podłogą wynosi \(0,2\). Oblicz pracę, jaką wykona siła tarcia w czasie przesuwania klocka z punktu \(A\) do punktu \(B\), odległego w linii prostej o \(2\,\mathrm{m}\):

  1. po linii prostej,
  2. po dwóch bokach kwadratu, dla którego linia łącząca punkty \(A\) i \(B\) jest jego przekątną.
  3. Czy siła tarcia jest zachowawcza?

 Wskazówka teoretyczna

 Teoria - praca stałej siły
Praca \(W\) stałej siły \(F\), działającej równolegle do kierunku przesuwania się ciała, równa jest

\(W=F\,S\),

gdzie \(S\) jest długością odcinka, o jaki ciało przesunięto.

Jeśli siła \(F\) tworzy z kierunkiem przesunięcia kąt \(\alpha\), to

\(W=F_sS=F\,S\,\cos\alpha\),

gdzie \(F_s\) jest składową siły równoległą do przesunięcia (styczna do toru).

Praca nie musi być wielkością dodatnią. Dla stałej siły, gdy kąt \(\alpha\) między przesunięciem a kierunkiem działania siły wynosi \(90^{\circ}\), to praca zeruje się, natomiast, gdy \(\alpha>90^{\circ}\), to praca ma wartość ujemną.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa klocka \(m=0,5\,\mathrm{kg}\),
- wartość współczynnika tarcia kinetycznego między klockiem a podłogą \(\mu=0,2\),
- odległość punktu \(B\) od punktu \(A\): \(L=2\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- praca wykonaną przez siłę tarcia podczas przesuwania po linii prostej \(W_1\),
- praca wykonaną przez siłę tarcia podczas przesuwania po bokach kwadratów \(W_2\).

Analiza sytuacji

Ponieważ siła tarcia, działająca na klocek, ma stałą wartość i stały kierunek względem przesunięcia (przeciwny do kierunku ruchu), dlatego pracę siły tarcia, przy przesunięciu ciała z punktu \(A\) do punktu \(B\) obliczymy, jako pracę stałej siły \(\vec{F}\):

\(W=\vec{F}\,\Delta \vec{S}=F\,\Delta S\,\cos\alpha\)

gdzie \(\Delta\vec{S}\) jest wektorem przesunięcia, a \(\alpha\) kątem między siłą a przesunięciem.

Siła tarcia w każdym punkcie toru ma stałą wartość \(T=\mu\,mg\) oraz kierunek przeciwny do kierunku przesunięcia tj, wektora prędkości \(\vec{v}\) lub wektora przesunięcia o \(\Delta\vec{S}\). Stąd mamy

\(W=T\,\Delta S\,\cos\alpha=\mu\,mg \Delta S\cos 180^{\circ}=-\mu\,mg\Delta S\)

Rozwiązanie

1. Obliczmy pracą wykonaną przez siły podczas przesunięciu klocka po linii prostej od punktu \(A\) do \(B\).

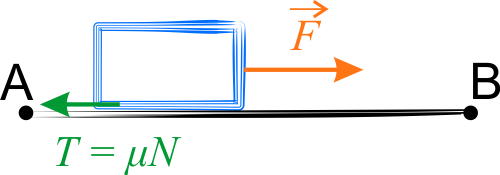
Rysunek

W tym przypadku na całej drodze wektor siły jest stały i równolegle skierowany do przesunięcia. Do powyższego równania podstawiamy \(S=L\) i otrzymujemy:

\(W_1=-\mu\,mg\,L\)

\(W_1=-0,2\cdot 0,5\cdot 10\cdot 2=-2\,\mathrm{J}\)

2. Obliczmy pracę wykonaną przy przesunięciu klocka od punktu \(A\) do punktu \(B\) po drodze będącej bokami kwadratu.

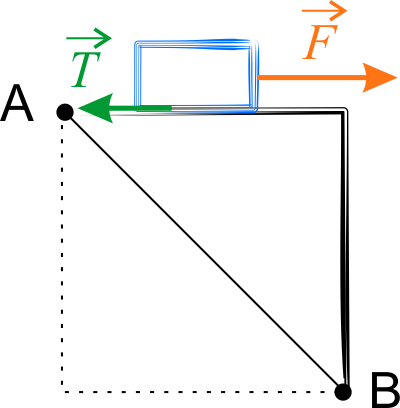
Rysunek

Zauważmy, że podczas przesuwania klocka po każdym z boków kwadratu, siła tarcia jest dalej równoległa do przesunięcia i tworzy z nim kąt \(180^{\circ}\). Praca na całej drodze będzie równa sumie prac wykonanych podczas przesuwania wzdłuż każdego z boków. Bok kwadratu o przekątnej \(L\) wynosi \(\displaystyle{L\frac{\sqrt{2}}{2}}\).

\(\displaystyle{W_2=\frac{\sqrt{2}}{2}\cdot L\,\mu\,mg\cdot \cos 180^{\circ}+\frac{\sqrt{2}}{2}\cdot L\,\mu\,mg\cdot \cos 180^{\circ}}\)

\(W_2=-\sqrt{2}\,\mu \,mg\,L\)

\(W_2=-\sqrt{2}\cdot 0,2\cdot 0,5\cdot 10\cdot 2\)

\(W_2=-2,8\,\mathrm{J}\)

3. Siła jest siłą zachowawczą, jeżeli praca tej siły między punktem początkowym a końcowym, po dowolnej drodze, jest taka sama. Licząc pracę sił tarcia po dwu różnych drogach otrzymaliśmy różne wyniki.

\(W_1\neq W_2\)

\(-2\,\mathrm{J}\neq -2,8\,\mathrm{J}\)

Wnioskujemy stąd, że siła tarcia nie jest siłą zachowawczą.

Odpowiedź

Praca, jaką wykona siła tarcia w czasie przesuwania klocka z punktu \(A\) do punktu \(B\) w przypadku, gdy klocek przesuwany jest po
1. linii prostej, wynosi \(W_1=-2\,\mathrm{J}\).
2. dwóch bokach kwadratu, dla którego linia łącząca punkty \(A\) i \(B\) jest jego przekątną, wynosi \(W_2=-2,8\,\mathrm{J}\).

Ponieważ \(W_1\neq W_2\), wnioskujemy stąd, że siła tarcia nie jest siłą zachowawczą.