Zadanie 4.1.1.5
Praca przy wyciąganiu kulki z cieczy
Kula o promieniu \(R\) pływa w cieczy o gęstości \(\rho\), przy czym jest w niej zanurzona do połowy swej objętości. Jaką pracę należy wykonać, aby wydobyć kulkę nad poziom cieczy?
Wskazówka teoretyczna
Teoria - praca zmiennej siły
Przez zmienną siłę rozumiemy siłę, której wartość wzdłuż drogi ulega zmianie lub zmienia się kąt zawarty między kierunkiem działania siły i kierunkiem przesunięcia. W takim przypadku dzielimy drogę na małe odcinki elementarne \(\mathrm{d}S\), na których siłę możemy traktować jako stałą. Liczymy pracę elementarną dla każdego z tych odcinków, korzystając ze wzoru na pracę stałej siły
a następnie takie prace sumujemy na całej drodze, co matematycznie odpowiada wyznaczeniu całki:
\(\mathrm{d}W=F\mathrm{d}S\),
a następnie takie prace sumujemy na całej drodze, co matematycznie odpowiada wyznaczeniu całki:
\(\displaystyle{W=\int_{0}^{S}F\,\mathrm{d}S}\)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- promień kuli \(R\),
- gęstość cieczy \(\rho\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- praca, jaką należy wykonać przy wydobywaniu kulki nad poziom cieczy \(W\).
Analiza sytuacji
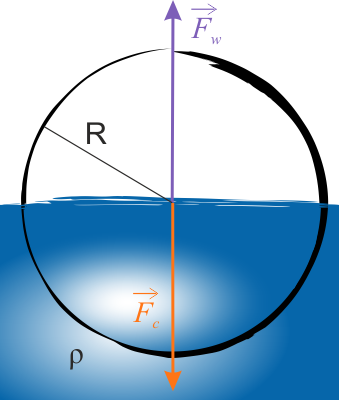
Na zanurzoną do połowy swojej objętości, pływającą kulkę, działają dwie równoważące się siły:
- siła ciężkości \(F_c\),
- siła wyporu \(F_w\) równa ciężarowi cieczy wypartej przez połowę objętości kulki \(\displaystyle{\frac{1}{2}\cdot \frac{4}{3}\pi R^3}\).
\(\displaystyle{F_w=\frac{2}{3}\pi R^3\cdot \rho\,g}\)
Z warunku równowagi mamy:
\(\displaystyle{F_c=F_w=\frac{2}{3}\pi R^3\cdot \rho\,g}\)
Przy wyciąganiu kulki z cieczy siła ciężkości oraz siła wyporu nie równoważ się wzajemnie i siła wypadkowa, działająca na kulkę wynosi
\(F=F_c-F_w(h)\)
gdzie siła wyporu \(F_w(h)\) zależy od głębokości zanurzenia kulki i wynosi \(F_w=V\rho\,g\), \(V\) jest objętością czaszy kulistej o wysokości \(h\) i promieniu \(R\).
Rozwiązanie
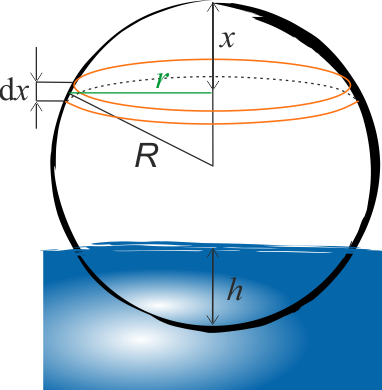
Wzór na objętość \(V\) można otrzymać symulując objętość \(\mathrm{d}V\) plasterków o promieniu \(r\) i grubości \(\mathrm{d}x\).
Objętość \(\mathrm{d}V\) wynosi:
\(\mathrm{d}V=\pi r^2\mathrm{d}x\)
Korzystając z twierdzenia Pitagorasa możemy zapisać:\(r^2+(R-x)^2=R^2\)
\[r^2=R^2-(R-x)^2\] \[r^2=R^2-(R^2-2Rx+x^2)\] \[r^2=\cancel{R^2}-\cancel{R^2}+2Rx-x^2\]
\(r^2=2Rx-x^2\)
Objętość czaszy kulistej o wysokości \(h\) równa jest następującej całce
\(\displaystyle{V=\pi\int_{0}^{h}\left ( 2Rx-x^2 \right )\mathrm{d}x}\)
\[\displaystyle{V=\pi\left [Rx^2-\frac{1}{3}x^3\right ]_0^h }\] \[\displaystyle{V=\pi\left ( Rh^2-\frac{1}{3}h^3 \right ) }\]
\(\displaystyle{V=\frac{1}{3}\pi h^2 \left (3R-h\right ) }\)
Zatem wypadkowa siła działająca na kulkę wynosi:
\(F=F_c-F_w\)
\[\displaystyle{F=\frac{2}{3}\pi R^3\rho\,g-V\rho\,g}\] \[\displaystyle{F=\frac{2}{3}\pi R^3\rho\,g-\frac{1}{3}\pi h^2 \left (3R-h\right )\rho\,g}\] \[\displaystyle{F=\frac{2}{3}\pi R^3\rho\,g-\frac{1}{3}\pi h^2 \left (3R-h\right )\rho\,g}\]
\(\displaystyle{F=\pi\rho\,g\left (\frac{2}{3}R^3-\frac{1}{3}h^2\left (3R-h\right )\right )}\)
Wiemy, że \(x=R-h\). Podstawiając \(h=R-x\) do wyrażenia na siłę wypadkową \(F\), otrzymujemy zależność \(F(x)\):
\(\displaystyle{F(x)=\pi\rho\,g\left (\frac{2}{3}R^3-\frac{1}{3}(R-x)^2\left (3R-R+x\right )\right )}\)
\[\displaystyle{F(x)=\pi\rho\,g\left (\frac{2}{3}R^3-\frac{1}{3}(R^2-2Rx+x^2)\left (2R+x\right )\right )}\] \[\displaystyle{F(x)=\pi\rho\,g\left (\frac{2}{3}R^3-\frac{1}{3}\left (2R^3+R^2x-4R^2x-2Rx^2+2Rx^2+x^3\right )\right )}\] \[\displaystyle{F(x)=\pi\rho\,g\left (\frac{2}{3}R^3-\frac{2}{3}R^3+\frac{3}{3}R^2x-\frac{1}{3}x^3\right )}\]
\(\displaystyle{F(x)=\pi\rho\,g\left (R^2x-\frac{1}{3}x^3\right )}\)
Siła wypadkowa rośnie w miarę wynurzania kulki. Aby wydobyć kulkę na powierzchnię należy działać na nią siłą równą, co do wartości, sile \(F\), ale przeciwnie skierowaną, na drodze \(R\). Zostanie przy tym wykonana praca:
\(\displaystyle{W=\int_{0}^{R}F(x)\,\mathrm{d}x }\)
\[\displaystyle{W=\int_{0}^{R}\pi\rho\,g\left (R^2x-\frac{1}{3}x^3\right )\,\mathrm{d}x }\] \[\displaystyle{W=\pi\rho\,g\left [\frac{1}{2}R^2x^2-\frac{1}{3}\cdot\frac{1}{4}x^4\right ]_0^R}\] \[\displaystyle{W=\pi\rho\,g\left (\frac{1}{2}R^2R^2-\frac{1}{12}R^4 \right ) }\]
\(\displaystyle{W=\frac{5}{12}\pi\rho\,gR^4}\)
Odpowiedź
Wydobycie kulki nad poziom cieczy wymaga pracy \(\displaystyle{W=\frac{5}{12}\pi\rho\,gR^4}\).