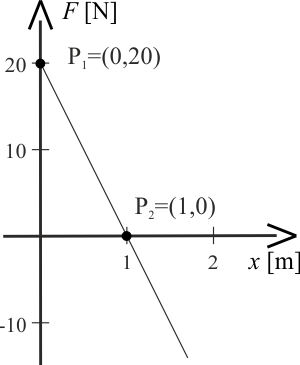Zadanie 4.1.1.6
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.1. Praca sił. Energia mechaniczna
  4. 4.1.1 Nauka
  5. Zadanie 4.1.1.6

 Zadanie 4.1.1.6

Praca - przemieszczenie w układzie współrzędnych
Pod działaniem siły \(F\) ciało porusza się wzdłuż osi \(x\). Na rysunku przedstawiono wykres zależności wartości siły \(F\) od położenia ciała. Wyznacz pracę wykonaną przez tę siłę na drodze \(1,5\,\mathrm{m}\). Obliczenia przeprowadź dwoma metodami: graficzną i przy pomocy definicji.

Rysunek

 Wskazówka teoretyczna

 Teoria - praca
Praca \(W\) stałej siły \(F\), działającej równolegle do kierunku przesuwania się ciała, równa jest

\(W=F\,S\),

gdzie \(S\) jest długością odcinka, o jaki ciało przesunięto.

Wzór na pracę ma prostą geometryczną interpretację. Mianowicie, na wykresie siły w zależności od przemieszczenia, miarą pracy jest pole powierzchni między krzywą siły a osią przemieszczeń.

Przez zmienną siłę rozumiemy siłę, której wartość wzdłuż drogi ulega zmianie lub zmienia się kąt zawarty między kierunkiem działania siły i kierunkiem przesunięcia. W takim przypadku dzielimy drogę na małe odcinki elementarne \(\mathrm{d}S\), na których siłę możemy traktować jako stałą. Liczymy pracę elementarną dla każdego z tych odcinków, korzystając ze wzoru na pracę stałej siły

\(\mathrm{d}W=F\mathrm{d}S\),

a następnie takie prace sumujemy na całej drodze, co matematycznie odpowiada wyznaczeniu całki:

\(\displaystyle{W=\int_{0}^{S}F\,\mathrm{d}S}\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- zależności siły od położenia ciała \(F(x)\).

Szukane:
- praca siły \(F\): \(W\).-

Metoda graficzna

Na ciało działa zmienna siła w kierunku osi \(x\). Pracę tej siły możemy wyznaczyć bądź to bezpośrednio z definicji poprzez całkowanie, bądź metodą graficzną, jako pole pod krzywą zależności siły od położenia, przy czym, jeśli krzywa leży powyżej osi to praca jest dodatnia, a gdy poniżej – ujemna.

Wyznaczmy najpierw wartość siły \(F\) dla \(x=1,5\,\mathrm{m}\). Jak wynika z rysunku przedstawionego w treści zadania, siła ta zmienia się liniowo. Mając dane dwa punkty tej prostej \(F_x(0)=20\,\mathrm{N}\) oraz \(F_x(1)=0\,\mathrm{N}\), łatwo jest wyznaczyć równanie tej prostej, czyli zależność wartości siły od położenia. Otrzymujemy:
 Równanie prostej można wyznaczyć na podstawie dwóch punktów \(P_1=(0,20)\) oraz \(P_2=(1,0)\) odczytanych z wykresu. Wartości te należy podstawić do równania prostej \(y=ax+b\): \[\begin{eqnarray} \begin{cases} 20 &=a\cdot 0+b\\ 0 &=a\cdot 1+b \end{cases} \end{eqnarray} \] \[\begin{eqnarray} \begin{cases} b &=20 \\ a &=-b \end{cases} \end{eqnarray} \] 

\(F_x(x)=-20x+20\,\mathrm{[N]}\)
\(F_x(x)=20\,(1-x)\,\mathrm{[N]}\)

gdzie \(x\) jest wyrażone w metrach, a stąd wartość siły dla \(x=1,5\,\mathrm{m}\) wynosi \(F(1,5)=-10\,\mathrm{N}\).

Praca siły \(F\) na drodze do jednego metra jest dodatnia, a dalej ujemna. Ponieważ pola powierzchni między krzywą zależności \(F (x)\) a osią \(x\) mają postać trójkątów, to łatwo jest obliczyć pracę. Oznaczając \(W_+\) - praca dla \(F > 0\) i \(W_-\) - praca dla \(F < 0\) mamy:

\(\displaystyle{W=W_++W_-=\frac{1}{2}\cdot 20\,\mathrm{N}\cdot 1\,\mathrm{m}+\frac{1}{2}\cdot (-10\,\mathrm{N})\cdot 0,5\,\mathrm{m} }\)
\(W=10-2,5=7,5\,\mathrm{J}\)

Obliczenia na podstawie definicji pracy

 Z definicji praca zmiennej siły działającej w kierunku osi \(x\), tj. \(F_x(x)\) od położenia \(x_1\) do \(x_2\) wynosi:

\(\displaystyle{W=\int_{x_1}^{x_2}F_x(x)\,\mathrm{d}x }\)
 \[\int \,\mathrm{d}x=x+C\] \[\int x^n\,\mathrm{d}x=\frac{1}{n+1}x^{n+1}+C, \; n\neq-1\] 
\(\displaystyle{W=\int_{0}^{1,5}20(1-x)\,\mathrm{d}x }\)

\(\displaystyle{W=\left [ 20\,(x-\frac{x^2}{2}) \right ]_0^{1,5} }\)

\(\displaystyle{W=20\,(1,5-\frac{1,5^2}{2})=7,5\,\mathrm{J} }\)

Odpowiedź

Praca wykonana przez siłę \(F\) wynosi \(W=7,5\,\mathrm{J}\).