Zadanie 4.2.1.1
Piłkę o masie \(0,1\,\mathrm{kg}\) upuszczono z wysokości \(5\,\mathrm{m}\). Wiemy, że po każdym odbiciu traci ona \(10\)% swojej energii mechanicznej.
a) Oblicz na, jaką wysokość wzniesie się piłka po drugim odbiciu.
b) Oblicz prędkość piłki tuż po trzecim odbiciu.
Wskazówka teoretyczna
Ogólne wyrażenie na energię piłki po \(n\)– tym odbiciu wynosi
gdzie \(q\) oznacza współczynnik strat energii. Energia całkowita, tuż po odbiciu piłki, jest równa energii kinetycznej piłki
a gdy piłka osiągnie maksymalną wysokość to energia całkowita piłki jest równa energii potencjalnej
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa piłki \(m=0,1\,\mathrm{kg}\),
- początkowa wysokość, z jakiej spadła piłka \(h=5\,\mathrm{m}\),
- strata energii mechanicznej po każdym odbiciu \(10\)%,
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- wysokość, na jaką wzniesie się piłka po drugim odbiciu \(h_2\),
- prędkość piłki tuż po trzecim odbiciu \(v_3\).
Analiza sytuacji
Piłka na wysokości \(5\,\mathrm{m}\) ma energię mechaniczną równą energii potencjalnej. Podczas spadku piłki następuje w całości zamiana jej energii potencjalnej na energię kinetyczną (zaniedbujemy pracę siły oporu powietrza). Przy każdym odbiciu następuje skokowo zamiana części energii mechanicznej na energię wewnętrzną (cieplną) podłogi i piłki, w związku z tym energia mechaniczna piłki maleje.
Początkowa energia mechaniczna \(E_0\) piłki równa jej początkowej energii potencjalnej, wynosi:
Po pierwszym odbiciu energia ta wynosi:
Po drugim odbiciu mamy
Po trzecim odbiciu mamy
Rozwiązanie
a) Wysokość \(h_2\), na jaką wzniesie się piłka po drugim odbiciu znajdujemy z faktu, że, po drugim odbiciu, energia całkowita piłki jest równa energii potencjalnej na maksymalnej wysokości piłki \(E_2=mgh_2\). Mamy więc:
b) Prędkość piłki tuż po trzecim odbiciu znajdujemy z tego faktu, że tuż po trzecim odbiciu energia całkowita jest równa energii kinetycznej piłki
Z zasady zachowania energii mamy
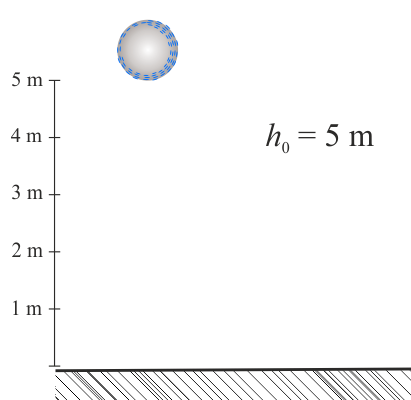
Piłka spada z wysokości \(h_0\).
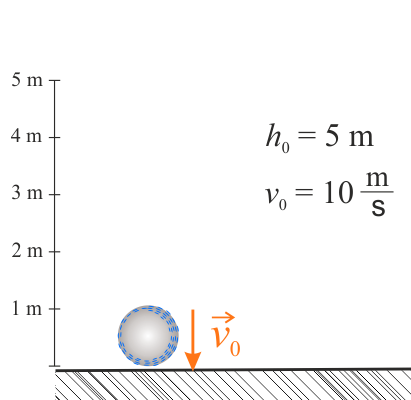
Piłka tuż przed zderzeniem piłka ma prędkość \(v_0\).
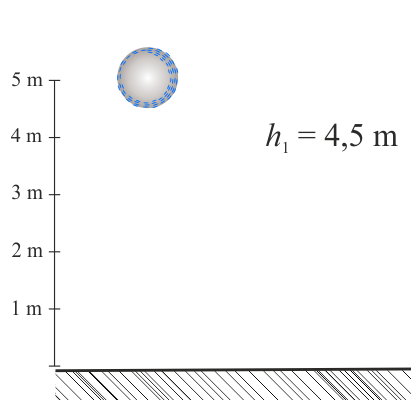
Piłka wzlatuje na wysokość \(h_1\) i zaczyna opadać w dół.
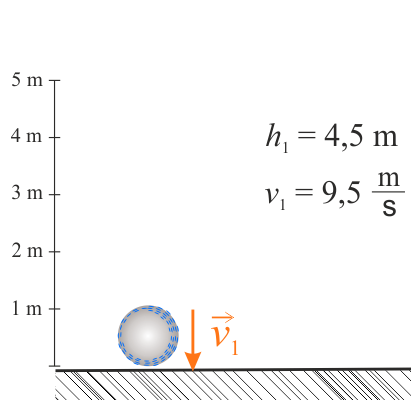
Piłka tuż przed zderzeniem piłka ma prędkość \(v_1\).
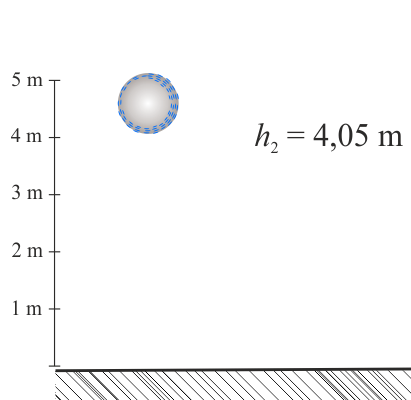
Piłka wzlatuje na wysokość \(h_2\) i zaczyna opadać w dół.
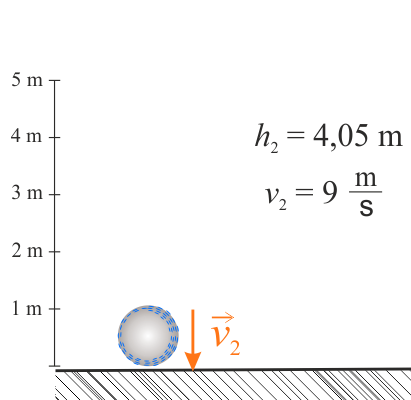
Piłka tuż przed zderzeniem piłka ma prędkość \(v_2\).
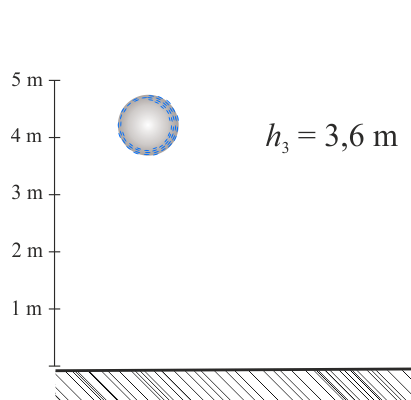
Piłka wzlatuje na wysokość \(h_3\) i zaczyna opadać w dół.
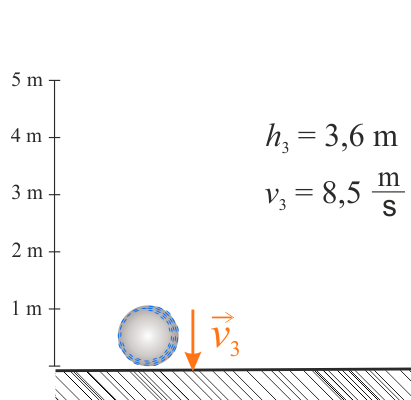
Piłka tuż przed zderzeniem piłka ma prędkość \(v_3\).
Odpowiedź
Piłka, po drugim odbiciu, wzniesie się na wysokość \(h_2=4,05\,\mathrm{m}\), natomiast wartość prędkości piłki tuż po trzecim odbiciu wynosi \(\displaystyle{v_3=8,54\,\mathrm{\frac{m}{s}}}\).
