Zadanie 4.2.1.2
Zmienny współczynnik tarcia
Ciało zsuwa się po powierzchni nachylonej pod kątem \(\alpha\) do poziomu. Współczynnik tarcia \(\mu\) zależy od przebytej drogi \(S\) przez ciało. Zależność tą opisuje formuła \(\mu(S)=b\,S\), gdzie \(b\) jest dodatnim współczynnikiem. Wyznacz drogę \(S_1\) przebytą przez ciało do momentu zatrzymania się oraz maksymalna prędkość ciała na drodze \(S_1\).
Wskazówka teoretyczna
Teoria - zasada zachowania energi
Zasada zachowania energii w polu sił zachowawczych:
Innymi słowy, każda zmiana energii kinetycznej \(E_k\) jest równoważona przez równą co do wartości, a przeciwną co do znaku zmianę energii potencjalnej \(E_p\) układu, tak że ich suma pozostaje przez cały czas stała:
\(\Delta E_p+\Delta E_k=0\).
Innymi słowy, każda zmiana energii kinetycznej \(E_k\) jest równoważona przez równą co do wartości, a przeciwną co do znaku zmianę energii potencjalnej \(E_p\) układu, tak że ich suma pozostaje przez cały czas stała:
\(E_k+E_p=const\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- kąt nachylenia równi \(\alpha\),
- zależność współczynnika tarcia od przebytej drogi \(\mu(S)=b\,S\), gdzie \(b\) jest dodatnim współczynnikiem.
Szukane:
- droga przebyta przez ciało do momentu zatrzymania się \(S_1\),
- maksymalna prędkość ciała na drodze \(S_1\): \(v_m\).
Analiza sytuacji
Na ciało zsuwające się po równi pochyłej działa siła ciężkości \(\vec{P}\) o wartości \(P=mg\) oraz siła tarcia \(\vec{T}\). Siłę ciężkości można rozłożyć na dwie składowe - styczną \(P_s\) oraz równoległą \(P_n\) do powierzchni równi.
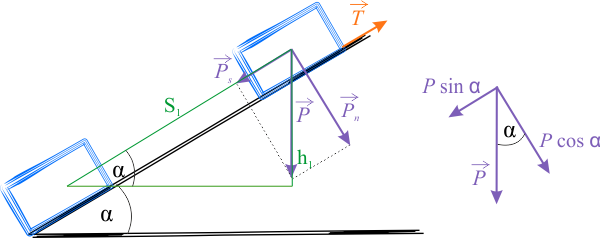
Z rysunku można odczytać, że \(P_s=mg\sin \alpha\) oraz \(P_n=mg\cos \alpha\). Z definicji siły tarcia wiemy, że \(T=\mu P_n=\mu mg\cos \alpha\). Wiemy również, że współczynnik tarcia \(\mu\) zależy od przebytej drogi, więc siła tarcia też jest funkcją tej drogi.
\(T(S)=b\,m\,g\cos \alpha \,S\)
Współczynnik tarcia rośnie wraz z przebytą drogą, więc ciało, w pewnym momencie, zatrzyma się. Wyznaczmy punk początkowy i końcowy, w którym ciało staje. Zsuwając się po pochyłości energia całkowicie zużyta jest na pracę przeciwko sile tarcia. Skorzystamy z zasady zachowania energii. Energia potencjalna na początku ruchu \(E_p=mgh_1\) (gdzie \(h_1\) oznacza różnicę poziomów miedzy położeniem początkowym a końcowym ciała) zostaje w całości zużyta na pracę \(W\) przeciwko sile tarcia na drodze \(S_1\), czyli do momentu zatrzymania się, gdyż w chwili zatrzymania się ciała energia kinetyczna \(E_k=0\). Ponieważ siła \(F_t\) zmienia się w czasie ruchu, więc korzystając z definicji pracy, otrzymujemy:
\(\displaystyle{W=\int_{0}^{S_1}T(S)\,\mathrm{d}S}\)
Przez zmienną siłę rozumiemy siłę, której wartość wzdłuż drogi ulega zmianie lub zmienia się kąt zawarty między kierunkiem działania siły i kierunkiem przesunięcia. W takim przypadku dzielimy drogę na małe odcinki elementarne \(\mathrm{d}S\), na których siłę możemy traktować jako stałą. Liczymy pracę elementarną dla każdego z tych odcinków, korzystając ze wzoru na pracę stałej siły \(\mathrm{d}W=F\mathrm{d}S\),a następnie takie prace sumujemy na całej drodze, co matematycznie odpowiada wyznaczeniu całki.
Rozwiązanie
Podstawiając wyrażenie, opisujące działanie siły tarcia, do definicji pracy, otrzymujemy:
\(\displaystyle{W=\int_{0}^{S_1}b\,m\,g\cos \alpha\,S\,\mathrm{d}S}\)
\[\displaystyle{W=b\,m\,g\cos \alpha\int_{0}^{S_1}S\,\mathrm{d}S}\] \[\displaystyle{W=b\,m\,g\cos \alpha\left [ \frac{1}{2}S^2 \right ]_0^{S_1} }\]
\(\displaystyle{W=\frac{1}{2}b\,m\,g\cos \alpha S_1^2}\)
Porównując energię potencjalną \(E_p\) z otrzymaną pracą mamy
\(\displaystyle{mgh_1=\frac{1}{2}b\,m\,g\cos \alpha S_1^2}\)
Wielkość \(h_1\) wyznaczamy z zależności \(\displaystyle{\sin\alpha=\frac{h_1}{S_1}}\) (zielony trójkąt na rysunku powyżej).\(\displaystyle{\cancel{mgS_1}\sin\alpha=\frac{1}{2}b\cancel{mg S_1}\,S_1\cos \alpha }\)
\(\displaystyle{\frac{2}{b}\frac{\sin\alpha}{\cos\alpha}=S_1 }\)
\(\displaystyle{S_1=\frac{2}{b}\operatorname{tg}{\alpha} }\)
W kolejnym kroku wyznaczymy zależność prędkości \(v\) ruchu ciała do przebytej drogi \(S\). W dowolnej chwili ruchu energia kinetyczna jest równa różnicy początkowej energii i pracy przeciwko sile tarcia.
\(E_k=E_p-W\)
Otrzymujemy zatem zależność
\(\displaystyle{\frac{mv^2}{2}=mgS\sin\alpha-\frac{1}{2}bmg\cos\alpha\,S^2 }\)
gdzie ostatni człon równania jest tym razem pracą wykonana po przebyciu drogi \(S\). Stąd
\(v=\sqrt{2gS\sin\alpha-bg\cos\alpha\,S^2 }\)
Aby wyznaczyć wartość prędkości maksymalnej należy obliczyć pochodną funkcji \(v(S)\) po \(S\) i przyrównać ją do zera.\(\displaystyle{\frac{\mathrm{d}v}{\mathrm{d} S}=\frac{1}{2\sqrt{2gS\sin\alpha-bg\cos\alpha\,S^2}}\cdot\left (2g\sin\alpha-2bgS\cos\alpha\right ) }\)
\(\displaystyle{\frac{g\left (\sin\alpha-bS\cos\alpha\right )}{\sqrt{2gS\sin\alpha-bg\cos\alpha\,S^2}}=0 }\)
Wyznaczona funkcja przyjmie wartość zero, wtedy gdy
\(\sin\alpha-bS\cos\alpha=0\)
Jak widać z powyższej zależności, prędkość jest maksymalna dla \(\displaystyle{S_1=\frac{\sin\alpha}{\cos\alpha}\cdot\frac{1}{b}=\frac{\operatorname{tg}{\alpha}}{b} }\) i wynosi
\(\displaystyle{v_m=\sqrt{2g\cdot\frac{\sin\alpha}{\cos\alpha}\cdot\frac{1}{b}\cdot \sin\alpha-bg\cos\alpha\cdot \frac{\sin^2\alpha}{\cos^2\alpha}\cdot \frac{1}{b^2}} }\)
\(\displaystyle{v_m=\sin\alpha\sqrt{\frac{2g}{b\cos\alpha}-\frac{g}{b\cos\alpha}} }\)
\(\displaystyle{v_m=\sin\alpha\sqrt{\frac{g}{b\cos\alpha}} }\)
Odpowiedź
Droga, przebyta przez ciało do momentu zatrzymania się, wynosi \(\displaystyle{S_1=\frac{2}{b}\operatorname{tg}{\alpha} }\), zaś maksymalna wartość prędkości na tej drodze przyjmuje postać \(\displaystyle{v_m=\sin\alpha\sqrt{\frac{g}{b\cos\alpha}} }\).