Zadanie 4.2.1.3
a) nie odpaść od pętli,
b) odpaść na wysokości \(1,8\,\mathrm{m}\)?
Wskazówka teoretyczna
Innymi słowy, każda zmiana energii kinetycznej \(E_k\) jest równoważona przez równą co do wartości, a przeciwną co do znaku zmianę energii potencjalnej \(E_p\) układu, tak że ich suma pozostaje przez cały czas stała:
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Doświadczenie
Odśrodkowa siła bezwładności i zasada zachowania energii (pętla z rynny i kulka).
Dane i szukane
Dane:
- promień pętli \(r=1,2\,\mathrm{m}\),
- wysokość, na jakiej klocek powinien odpaść od pętli w punkcie b). \(h=1,8\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- wysokość, jakiej klocek powinien się ześliznąć, aby nie odpaść od pętli: \(H_1\),
- wysokość, jakiej klocek powinien się ześliznąć, aby odpaść od pętli na wysokości \(h\): \(H_2\).
Analiza sytuacji
Pomiędzy zsuwającym się klockiem a rynną nie działa siła tarcia, dlatego do rozwiązania zadania skorzystamy z zasady zachowania energii mechanicznej klocka. Ruch klocka wzdłuż pętli jest ruchem krzywoliniowym po okręgu. Rozpatrzmy ten ruch w inercjalnym układzie odniesienia. Zakrzywienie toru związane jest z działaniem na klocek siły dośrodkowej. Siła ta jest wypadkową siły ciężkości – przypadek a) lub jego składowej – przypadek b) oraz siły reakcji podłoża (rynny), której wartość jest równa wartości siły nacisku klocka na rynnę. Aby klocek nie oderwał się od rynny, siła nacisku klocka na rynnę musi być większa od zera. W momencie odrywania się klocka od rynny siła nacisku jest równa zero.
Rozwiązanie a)
Sytuację opisaną w zadaniu przedstawia rysunek.
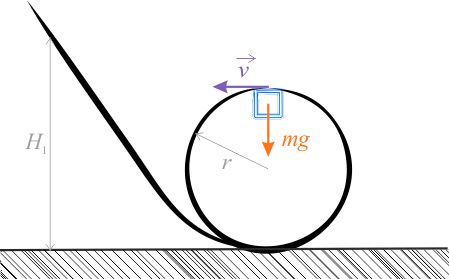
Klocek ześlizgując się z wysokości \(H_1\) zamienia swoją energię potencjalną najpierw na kinetyczną, a następnie znów częściowo energię kinetyczną na energię potencjalną. Gdy klocek znajduje się w najwyższym punkcie pętli mamy:
gdzie \(v_1\) oznacza prędkość w najwyższym punkcie pętli.
Dzieląc obustronnie przez \(mg\) otrzymujemy:
W najwyższym punkcie siła nacisku \(N\) jest równa zero, a co za tym idzie, wartość siły reakcji \(R\) podłoża również wynosi zero, czyli wypadkowa siła, pełniąca rolę siły dośrodkowej, jest to siła ciężkości o wartości \(mg\).
Korzystając z definicji siły dośrodkowej mamy:
Taką wartość prędkości musi mieć klocek, aby siła nacisku na rynnę była równa zero. Przy większych prędkościach klocek będzie naciskał na rynnę, przy mniejszych wcześniej od niej odpadnie.
Wyznaczmy teraz wysokość, z jakiej musi zsuwać się klocek, aby w najwyższym punkcie pętli wartość jego prędkości była równa \(v_1\). Do wyprowadzonej wcześniej formuły na \(H_1\) podstawiamy prędkość i mamy
Rozwiązanie b)
Sytuację opisaną w zadaniu dla przypadku b) przedstawia rysunek.
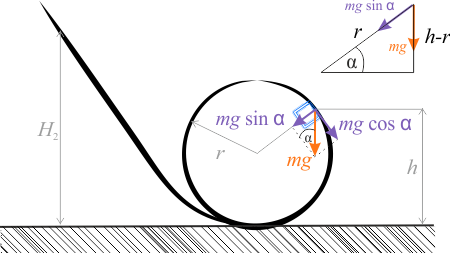
Klocek ześlizgując się z wysokości \(H_2\) zamienia swoją energię potencjalną najpierw na kinetyczną, a następnie znów częściowo energię kinetyczną na energię potencjalną. Gdy klocek znajduje się na wysokości \(h\), z prawa zachowania energii mamy:
gdzie \(v_2\) - prędkość na wysokości \(h\). Stąd
Wyznaczmy teraz prędkość \(v_2\) taką, że na wysokości \(h\) następuję oderwanie się klocka od pętli. Na tej wysokości rolę siły dośrodkowej spełnia składowa siły ciężkości do środka pętli \(mg\sin\alpha\) (patrz rysunek), gdyż siła reakcji pętli jest równa zero. Korzystając z definicji siły dośrodkowej mamy:
Na powyższym rysunku został narysowany trójkąt pomocniczy, który ułatwia zapisanie zależności \(\displaystyle{\sin\alpha=\frac{h-r}{r} }\). Po podstawieniu i kilku \[\displaystyle{H_2=h+\frac{r\cdot \frac{h-r}{r}}{2}}\] \[\displaystyle{H_2=h+\frac{h-r}{2}}\] \[\displaystyle{H_2=\frac{2h}{2}+\frac{h-r}{2}}\] otrzymujemy
Odpowiedź
Jeżeli puścimy klocek z wysokości \(H_1=3\,\mathrm{m} \), to nie wypadnie on z pętli, jeżeli natomiast wysokość tą zmniejszymy do wartości \(H_2=2,1\,\mathrm{m} \), odpadnie on od pętli na wysokości \(1,8\,\mathrm{m} \).
