Zadanie 4.2.1.4
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.2. Zasada zachowania energi
  4. 4.2.1 Nauka
  5. Zadanie 4.2.1.4

 Zadanie 4.2.1.4

Skok na sprężystej linie
Zawodnik o masie \(64\,\mathrm{kg}\) wykonuje skok na linie z mostu. Ma on przywiązaną do nóg sprężystą linę (zamocowaną drugim końcem do mostu) o długości \(12\,\mathrm{m}\) i wartości współczynnika sprężystości \(\displaystyle{200\,\mathrm{\frac{N}{m}} }\). Zawodnik przechylając się rozpoczyna swobodne spadanie w dół. Po wyprostowaniu lina zaczyna się rozciągać i hamuje ruch zawodnika. Wykaż, że maksymalne wydłużenie liny podczas skoku wynosi około \(12,6\,\mathrm{m}\).

 Wskazówka teoretyczna

 Teoria - zasada zachowania energii
Zasada zachowania energii w polu sił zachowawczych:

\(\Delta E_p+\Delta E_k=0\).

Innymi słowy, każda zmiana energii kinetycznej \(E_k\) jest równoważona przez równą co do wartości, a przeciwną co do znaku zmianę energii potencjalnej \(E_p\) układu, tak że ich suma pozostaje przez cały czas stała:

\(E_k+E_p=const\).

Energia potencjalna sprężystości ma postać

\(\displaystyle{E_p=\frac{kx^2}{2}}\)

gdzie \(k\) jest współczynnikiem proporcjonalności między siłą a wychyleniem, a \(x\) - wychyleniem z położenia równowagi.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa zawodnika \(m=64\,\mathrm{kg}\),
- długość liny \(l=12\,\mathrm{m}\),
- współczynnik sprężystości liny \(\displaystyle{k=200\,\mathrm{\frac{N}{m}} }\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- maksymalne wydłużenie liny \(x\).

Analiza sytuacji

Zakładamy, że siła oporu powietrza, działająca na skoczka podczas jego ruchu, jest do pominięcia i jedynymi siłami są: siła ciężkości i siła sprężystości liny. Dodatkowo pominiemy ciężar liny i skończone rozmiary zawodnika – będziemy go traktować jako punkt materialny. W czasie spadania i rozciągania liny, energia potencjalna i kinetyczna zawodnika zostają zamienione na pracę przeciwko silę sprężystości liny.

Do rozwiązania zadania skorzystamy z zasady zachowania energii mechanicznej, gdyż siły działające na zawodnika – siła ciężkości i sprężystości liny są  Jeśli w każdym punkcie przestrzeni zostanie określona dana siła (co do wartości i kierunku), to mówimy o polu danej siły. Pole sił jest polem sił zachowawczych, jeśli praca potrzebna na przesunięcie ciała z dowolnego punktu \(A\) do dowolnego punktu \(B\) nie zależy od drogi, po jakiej ciało będzie przesuwane. 

Opis matematyczny

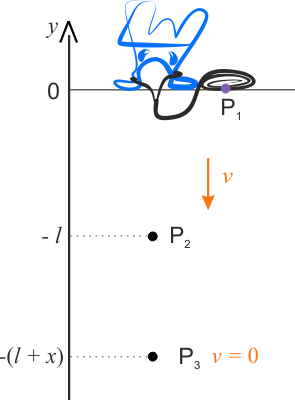
Sytuację opisaną w zadaniu przedstawia rysunek, na którym wprowadzono jednowymiarowy układ współrzędnych z osią \(y\) skierowaną pionowo i mającą swój początek na poziomie powierzchni mostu. Zakładamy też, że energia potencjalna zawodnika na poziomie powierzchni mostu – w punkcie \(P_1\), jest równa zeru, wtedy energia potencjalna ciężkości podczas skoku jest ujemna. W punkcie \(P_2\) w momencie, kiedy lina jest wyprostowana, ale jeszcze nie napięta wynosi ona \(-mgl\), w punkcie \(P_3\) w momencie, kiedy lina jest maksymalne wydłużona wynosi ona \(-mg(l+x)\). Energia kinetyczna najpierw rośnie do maksymalnej wartości, a następnie maleje do zera dla maksymalnego wydłużenia liny. Energia potencjalna sprężystości zaczyna rosnąć od zera, kiedy lina jest wyprostowana, ale jeszcze nie napięta do wartości maksymalnej \(\displaystyle{\frac{kx^2}{2}}\). Z zasady zachowania energii mechanicznej zawodnika w punktach \(P_1\) i \(P_3\) mamy, że \(E_{P1}=E_{P3}\), czyli:

\(\displaystyle{0=-mg(l+x)+\frac{kx^2}{2}}\)

Rysunek

Rozwiązanie

Po przekształceniach wyjściowego równania, otrzymujemy równanie kwadratowe postaci:

\(\displaystyle{\frac{k}{2}x^2-mgx-mgl=0}\)

Otrzymaliśmy równanie kwadratowe, którego wyróżnik wynosi:
\(\Delta=(mg)^2+2kmgl\)

Pierwiastki równania \(x_1\) oraz \(x_2\) mają postać:

\(\displaystyle{x_1=\frac{mg+\sqrt{(mg)^2+2kmgl}}{k} }\) oraz \(\displaystyle{x_2=\frac{mg-\sqrt{(mg)^2+2kmgl}}{k} }\)

Wartość drugiego pierwiastka jest ujemna, więc, jako niefizyczną, odrzucamy ją. Po podstawieniu liczb otrzymujemy

\(\displaystyle{x_1=\frac{64\cdot 10+\sqrt{(64\cdot 10)^2+2\cdot 200\cdot 64\cdot 10\cdot 12}}{200} }\)

\(\displaystyle{x_1=12,6\,\mathrm{m} }\)
 \[\displaystyle{\left (\frac{kg\cdot m}{s^2}+\sqrt{\frac{kg^2m^2}{s^4}+\frac{N\cdot kg\cdot m}{s^2}}\right )\cdot\frac{m}{N}=}\] \[\displaystyle{=\left ( N+\sqrt{N^2+N\cdot N}\right )\cdot\frac{m}{N}=}\] \[\displaystyle{=N\cdot\frac{m}{N}=m}\] 
Zatem maksymalne wydłużenie liny podczas skoku zawodnika wynosi \(12,6\,\mathrm{m}\).

Zauważmy, że maksymalna prędkość skoczka (a co za tym idzie energia kinetyczna) w momencie, kiedy lina jest wyprostowana, ale jeszcze nie napięta nie jest maksymalną prędkością zawodnika. Prędkość (energia kinetyczna) podczas wydłużania liny jeszcze rośnie. Osiąga wartość maksymalną, gdy siła sprężystości zrównoważy się z siłą grawitacji (punkt równowagi dla ruchu drgającego dla odległości \( l+h\) ), a dopiero później maleje.
Maksymalną prędkość skoczka wyznaczamy z warunku \(E_p=E_k\)

\[\displaystyle{mg\left (l+h\right)-\frac{1}{2}kh^2=\frac{mv^2}{2}}\]
Rozciąganie liny powoduje zmniejszanie się przyspieszenia skoczka.
Po przekształceniach otrzymujemy równanie na prędkość zależną od \(h\):
\[ \displaystyle{v(h)=\sqrt{2g\left ( l+h\right )-\frac{k}{m}h^2 } }\]
Obliczając pochodną tej funkcji otrzymamy odległość, przy której wartość prędkości jest maksymalna.
\[ \displaystyle{\frac{\mathrm{d} v}{\mathrm{d} h} = \frac{1}{2}\cdot \frac{2g-2\frac{k}{m}h}{\sqrt{2gl+2gh-\frac{k}{m}h^2}}} \]
Pochodna jest równa zeru, gdy \(h=g\frac{m}{k}\), a dla danych z zadania otrzymujemy:
\[h=10\cdot \frac{64}{200}=3,2\,\mathrm{m}\]
Maksymalną wartość prędkości obliczamy:
\[ \displaystyle{v(3,2)=\sqrt{2g\left ( l+h\right )-\frac{k}{m}h^2 }=\sqrt{2\cdot 10\left ( 12+3,2 \right )-\frac{200}{64}\cdot (3,2)^2 } }\]\[\displaystyle{v_{max}=16,5\,\mathrm{\frac{m}{s}} }\]

Odpowiedź

Maksymalne wydłużenie liny podczas skoku zawodnika wynosi \(12,6\,\mathrm{m}\).