Zadanie 4.3.2.4
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.3. Pola sił
  4. 4.3.2 Trening
  5. Zadanie 4.3.2.4

 Zadanie 4.3.2.4

Praca w polu sił
Dane jest pole sił: \(\vec{F}=(4xy^2,\;2y )\,\mathrm{N}\).

1. Oblicz prace sił pola przy przesuwaniu cząstki z położenia \(A=(0,1)\,\mathrm{m}\) do położenia \(B=(2,0)\,\mathrm{m}\). Zakładamy przy tym, że praca jest wykonana:
a) po linii prostej \(y=-0,5x+1\),
b) po elipsie \(\displaystyle{\frac{x^2}{4}+y^2=1 }\).

2. Czy to pole jest potencjalne?
Rysunek
Tor ruchu cząstki podczas przesuwania jej z punktu \(A\) do \(B\) po lini prostej (pomarańczowy odcinek) oraz po elipsie (niebieski fragment elipsy).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- wektor określający pole sił \(\vec{F}=(4xy^2,\;2y)\,\mathrm{N}\),
- współrzędne punktu początkowego \(A=(0,1)\,\mathrm{m}\),
- współrzędne punktu końcowego \(B=(2,0)\,\mathrm{m}\).

Szukane:
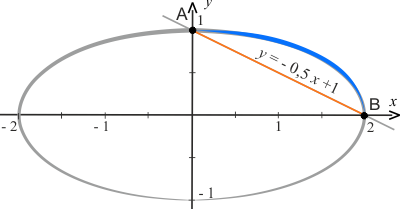
- praca sił pola przy przesuwaniu cząstki po linii prostej \(y=-0,5x+1\): \(W_1\),
- praca sił pola przy przesuwaniu cząstki po elipsie \(\displaystyle{\frac{x^2}{4}+y^2=1 }\): \(W_2\).

Odpowiedź

Poszczególne prace wynoszą: \(\displaystyle{W_1=\frac{1}{3}\,\mathrm{J} }\), \(\displaystyle{W_2=3\,\mathrm{J} }\). Jak widać praca zależy od drogi, po której jest wykonywana \(W_1\neq W_2\), stąd pole sił zadane siłą postaci \(\vec{F}=(4xy^2,\;2y )\,\mathrm{N}\) nie jest polem potencjalnym.

Polecenie

Wybierz jedno prawidłowe stwierdzenie, spośród dwóch przedstawionych poniżej.

Stwierdzenie 1 z 2

Zgodnie z definicją, praca przy przesuwaniu cząstki z położenia \(A\) do położenia \(B\) wyraża się wzorem

\(\displaystyle{W=\int_{(0,1)}^{(2,0)}(4xy^2\,\mathrm{d}x+2y\,\mathrm{d}y)}\)

Odpowiedź prawidłowa

Stwierdzenie 2 z 2

Zgodnie z definicją, praca przy przesuwaniu cząstki z położenia \(A\) do położenia \(B\) wyraża się wzorem

\(\displaystyle{W=\int_{(0,1)}^{(2,0)}((4xy^2+\frac{x^2}{4})\,\mathrm{d}x+(2y+y^2)\,\mathrm{d}y)}\)

Odpowiedź nieprawidłowa

Polecenie

Wyznacz prace sił pola przy przesuwaniu cząstki po linii prostej \(y=-0,5x+1\). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{W_1=\frac{1}{3}\,\mathrm{J}}\)

Odpowiedź prawidłowa

Wybór 2 z 4

\(\displaystyle{W_1=\frac{1}{2}\,\mathrm{J}}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{W_1=\frac{3}{4}\,\mathrm{J}}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{W_1=\frac{5}{3}\,\mathrm{J}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Zgodnie z definicją, praca przy przesuwaniu cząstki z położenia \(A\) do położenia \(B\) wyraża się wzorem

\(\displaystyle{W=\int_{(0,1)}^{(2,0)}(4xy^2\,\mathrm{d}x+2y\,\mathrm{d}y)}\)

Jeżeli praca jest wykonana po drodze, dla której \(y=-0,5x+1\), wówczas wzór na pracę można zapisać w postaci:

\(\displaystyle{W_1=\int_0^2 4x\,(-\frac{1}{2}x+1)^2\,\mathrm{d}x+\int_1^02y\,\mathrm{d}y}\)
 \[\displaystyle{W_1=\int_0^2 4x\,(\frac{1}{4}x^2-x+1)\,\mathrm{d}x+\left [ y^2 \right ]_1^0}\] \[\displaystyle{W_1=\left [\frac{1}{4}x^4-4\cdot\frac{1}{3}x^3+4\cdot \frac{1}{2}x^2\right ]_0^2-1}\] \[\displaystyle{W_1=\frac{1}{4}\cdot 2^4-\frac{4}{3}\cdot 2^3+2\cdot 2^2-1=\frac{1}{3}}\] 
\(\displaystyle{W_1=\frac{1}{3}\,\mathrm{J} }\)

Polecenie

Wyznacz prace sił pola przy przesuwaniu cząstki po elipsie \(\displaystyle{\frac{x^2}{4}+y^2=1 }\). Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(W_2=1\,\mathrm{J}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(W_2=2\,\mathrm{J}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(W_2=3\,\mathrm{J}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(W_2=4\,\mathrm{J}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Jeżeli praca jest wykonana po drodze, dla której \(\displaystyle{y^2=1-\frac{x^2}{4}}\), wówczas wzór na pracę można zapisać w postaci:

\(\displaystyle{W_2=\int_0^2 4x\,(1-\frac{x^2}{4})\,\mathrm{d}x+\int_1^02y\,\mathrm{d}y}\)
 \[\displaystyle{W_2=\int_0^2 (4x-x^3)\,\mathrm{d}x+\left [ y^2 \right ]_1^0}\] \[\displaystyle{W_2=\left [2x^2-\frac{1}{4}x^4\right ]_0^2+(0-1) }\] \[\displaystyle{W_2=2\cdot 2^2-\frac{1}{4}\cdot 2^4-1=3 }\] 
\(W_2=3\,\mathrm{J}\)

Odpowiedź

Poszczególne prace wynoszą: \(\displaystyle{W_1=\frac{1}{3}\,\mathrm{J} }\), \(\displaystyle{W_2=3\,\mathrm{J} }\). Jak widać praca zależy od drogi, po której jest wykonywana \(W_1\neq W_2\), stąd pole sił zadane siłą postaci \(\vec{F}=(4xy^2,\;2y )\,\mathrm{N}\) nie jest polem potencjalnym.