Rozwiązanie

Przy braku sił zewnętrznych, takich jak siła ciężkości i opory uchu, pęd układu złożonego z rakiety i wyrzuconych gazów musi być zachowany.

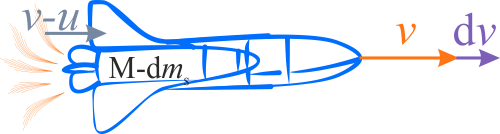
Na rysunku pokazana jest rakieta w pewnej chwili \(t+\mathrm{d} t\) po wyrzuceniu elementarnej porcji spalonych gazów \(\mathrm{d}m_s=r\mathrm{d} t\), w nieruchomym układzie współrzędnych. Ponieważ prędkość gazów względem rakiety wynosi \(u\) to w układzie nieruchomym, w którym rakieta porusza się z szybkością \(v\) ich prędkość wynosi \(v-u\). Stosują zasadę zachowania pędu, mamy:


 Przekształcenia  \[Mv=Mv+M\mathrm{d}v-\mathrm{d}m_sv-\mathrm{d}m_s\mathrm{d}v+\mathrm{d}m_sv-\mathrm{d}m_su\] \[0=M\mathrm{d}v-\mathrm{d}m_s\mathrm{d}v-\mathrm{d}m_su\] 

W nawiasie po lewej stronie równania decydującym składnikiem jest masa rakiety \(M\), toteż masę gazów wyrzucanych w czasie \(\mathrm{d}t\) można pominąć


Dzieląc otrzymane równanie obustronnie przez \(\mathrm{d}t\) i \(M\) otrzymujemy wzór na przyspieszenie rakiety


W uzyskanym wzorze \(M\) jest masą rakiety, która zmienia się w czasie. W związku z tym przyspieszenie \(a\) będzie również zależne od czasu.
Przyspieszenie początkowe rakiety będzie wynosić:


ponieważ masa rakiety na początku wynosiła \(M_0\).
Równanie różniczkowe wiążące szybkość rakiety z jej zmienną masa otrzymujemy po skorzystaniu ze związku \(\mathrm{d}m_s=-\mathrm{d}M\), czyli z tego, że elementarna ilość wyrzuconych gazów równa się przyrostowi masy rakiety ze znakiem minus.


Po scałkowaniu i uwzględnieniu warunków początkowych (dla \(t=0\), \(M=M_0\) i \(v=0\) ), otrzymujemy:

 Przekształcenia  \[\displaystyle{\int\mathrm{d}v=-u\int\frac{\mathrm{d}M}{M} }\] \[v=-u\,\ln M+C\] Z warunków początkowych mamy \[0=-u\,\ln M_0+C\] \[C=u\,\ln M_0\] \[v=-u\,\ln M+u\,\ln M_0\] 

Prędkość możemy wyrazić jako funkcję czasu. W tym celu należy znaleźć zależność masy rakiety od czasu.


Po scałkowaniu otrzymujemy


gdzie \(C\) jest stałą, która z warunków początkowych \((M_0=-r\cdot 0+C\)) wynosi \(M_0)\).


Teraz równane na prędkość ma postać