Zadanie 4.4.1.6
Zderzenie niecentralne
Pokaż, że w przypadku sprężystego zderzenia niecentralnego dwóch kul o jednakowych masach, z których jedna spoczywała, kąt jaki utworzą wektory prędkości po zderzeniu, wynosi \(90^{\circ}\).
Wskazówka teoretyczna
Teoria - zasada zachowania pędu
Zasada zachowania pędu.
Pęd zamkniętego układu ciał nie zmienia się z upływem czasu.
Zasadę te można też zapisać jako:
Suma pędów wszystkich ciał układu w momencie początkowym równa się sumie pędów tych ciał w dowolnym momencie późniejszym.
Pęd zamkniętego układu ciał nie zmienia się z upływem czasu.
\(\displaystyle{\frac{\mathrm{d}\vec{p} }{\mathrm{d} t}=0}\)
czyli \(\vec{p}=const\)Zasadę te można też zapisać jako:
Suma pędów wszystkich ciał układu w momencie początkowym równa się sumie pędów tych ciał w dowolnym momencie późniejszym.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masy kul \(m_1=m_2=m\),
- prędkość przed zderzeniem pierwszej kuli \(v\).
Szukane:
- wykazanie, że kąt, jaki utworzą wektory prędkości po zderzeniu, wynosi \(90^{\circ}\).
Analiza sytuacji
Oznaczmy przez \(\vec{v}\) prędkość kuli poruszającej się przed zderzeniem.

\(\vec{v}_1\) obrazuje prędkość kulki pierwszej po zderzeniu, natomiast \(\vec{v}_2\) oznacza prędkość drugiej kulki po zderzeniu.
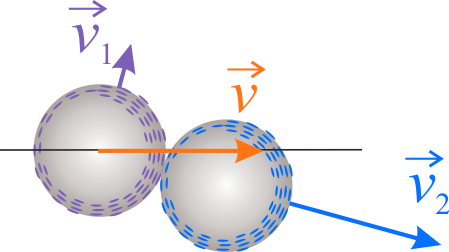
Z zasady zachowania pędu wynika, że pęd układu dwóch kulek przed zderzeniem wynosi \(\vec{p}=m\vec{v}\) jest równy pędowi układu po zderzeniu
\(\vec{p}_1+\vec{p}_2=m\vec{v}_1+m\vec{v}_2\)
Zatem
\(m\vec{v}=m\vec{v}_1+m\vec{v}_2\)
\(\vec{v}=\vec{v}_1+\vec{v}_2\)
Wektor \(\vec{v}\) możemy rozłożyć na dwie składowe \(\vec{v}_1\) i \(\vec{v}_2\).
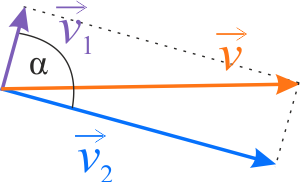
Zgodnie z twierdzeniem cosinusów dla długości tych wektorów można napisać równanie
\(v=\sqrt{v_1^2+v_2^2-2v_1v_2\cos\alpha}\)
W zderzeniu sprężystym zachowana jest energia kinetyczna układu dwóch kulek
\(\displaystyle{E_k=\frac{mv^2}{2} }\)
Po zderzeniu całkowita energia kinetyczna wyraża się zależnością
\(\displaystyle{E_{k1}+E_{k2}=\frac{mv_1^2}{2}+\frac{mv_2^2}{2} }\)
Zatem
\(\displaystyle{\frac{mv^2}{2}=\frac{mv_1^2}{2}+\frac{mv_2^2}{2} }\)
\(v^2=v_1^2+v_2^2\)
Rozwiązanie
Z zasady zachowania pędu otrzymaliśmy zależność
\(\vec{v}=\vec{v}_1+\vec{v}_2\)
A po zastosowaniu twierdzenia cosinusów otrzymaliśmy \(v=\sqrt{v_1^2+v_2^2-2v_1v_2\cos\alpha}\)
Z zasady zachowania energii mamy
\(v^2=v_1^2+v_2^2\)
\(v=\sqrt{v_1^2+v_2^2}\)
Porównując ostatnią zależność, z tą wynikającą z zasady zachowania pędu, mamy
\(\sqrt{v_1^2+v_2^2}=\sqrt{v_1^2+v_2^2-2v_1v_2\cos\alpha}\)
Stąd wynika, że \(2v_1v_2\cos\alpha=0\), czyli \(\cos\alpha=0\). Równanie to jest spełnione, w naszym zadaniu, dla \(\alpha=90^{\circ}\).
Informacja
Poniżej znajduje się animacja ilustrująca zderzenie niecentralne dwóch kul o takich samych masach. Animację uruchamia okrągły przycisk z białym trójkątem, umieszczony pod rysunkiem.
Odpowiedź
dd
