Zadanie 4.4.1.5
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.4. Zasada zachowania pędu
  4. 4.4.1 Nauka
  5. Zadanie 4.4.1.5

 Zadanie 4.4.1.5

Cząstki po zderzeniu poruszają się pod katem
Cząstka o masie \(m_1\) i prędkości \(v_1\) zderza się doskonale sprężyście z inną cząstką o masie \(m_2=3m_1\), znajdującą się w spoczynku \((v_0=0)\). Po zderzeniu cząstka o masie \(m_2\) porusza się pod kątem \(\alpha_2=45^{\circ}\) względem pierwotnego kierunku cząstki o masie \(m_1\). Znajdź kąt odchylenia \(\alpha_1\) masy \(m_1\) oraz końcowe prędkości cząstek \(u_1\) i \(u_2\).

 Wskazówka teoretyczna

 Teoria - zasada zachowania pędu
Zasada zachowania pędu.
Pęd zamkniętego układu ciał nie zmienia się z upływem czasu.

\(\displaystyle{\frac{\mathrm{d}\vec{p} }{\mathrm{d} t}=0}\)
czyli \(\vec{p}=const\)

Zasadę te można też zapisać jako:
Suma pędów wszystkich ciał układu w momencie początkowym równa się sumie pędów tych ciał w dowolnym momencie późniejszym.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa cząstki pierwszej \(m_1\),
- prędkość cząstki pierwszej \(v_1\)
- masa cząstki drugiej \(m_2=3m_1\),
- prędkość cząstki drugiej \(v_2\),
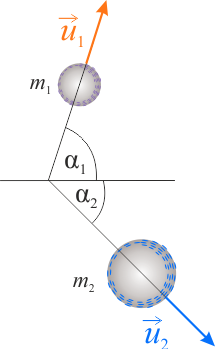
- kąt odchylenia toru ruchu cząstki drugiej \(\alpha_2=45^{\circ}\).

Szukane:
- kąt odchylenia toru ruchu cząstki pierwszej \(\alpha_1\),
- końcowa prędkość cząstki pierwszej \(u_1\),
- końcowa prędkość cząstki drugiej \(u_2\).

Rysunek 1
Przed zderzeniem

Analiza sytuacji

Korzystamy z zasady zachowaniu pęd dla układu dwóch zderzających się cząstek, porównują pęd całkowity przed zderzeniem z pędem całkowitym układu po zderzeniu kul:

\(m_1\vec{v}_1=m_2\vec{u_2}+m_1\vec{u}_1\)

Po skorzystaniu z zależności \(m_2=3m_1\) i obustronnym podzieleniu powyższego równania przez \(m_1\), mamy:

\(\vec{v}_1=\vec{u_1}+3\vec{u}_2\)

Wiemy, że zderzenie było zderzeniem sprężystym, a więc obowiązuje również w tym przypadku zasada zachowania energii kinetycznej

\(\displaystyle{\frac{m_1v_1^2}{2}=\frac{m_1u_1^2}{2}+\frac{m_2u_2^2}{2}}\)

Po uproszczeniu, mamy

\(v_1^2=u_1^2+3u_2^2\)

Rysunek 2
Po zderzeniu

Rozwiązanie

W celu wykonania dalszych obliczeń należy powyższe równania wektorowe rozpisać na równania dla poszczególnych składowych. Kierunki osi współrzędnych dobieramy w taki sposób, aby oś \(x\) pokrywała się z kierunkiem ruchu masy \(m_1\) przed zderzeniem, a oś \(y\) jest do niego prostopadła. Równania dla współrzędnych wektorów wyznaczonych dla tych kierunków mają postać:

\(\begin{eqnarray} \begin{cases} v_1 &=u_1\cos\alpha_1+3u_2\cos\alpha_2\\ 0 &=u_1\sin\alpha1-3u_2\sin\alpha_2 \end{cases} \end{eqnarray} \)

Do wyznaczonych równań wstawiamy wartość kąta \(\alpha_2=45^{\circ}\) i co za tym idzie \(\displaystyle{\sin\alpha_2=\cos\alpha_2=\frac{\sqrt{2}}{2}}\) i mamy:

\(\begin{eqnarray} \begin{cases} v_1 &=u_1\cos\alpha_1+3\cdot \frac{\sqrt{2}}{2}u_2\\ 0 &=u_1\sin\alpha_1-3\cdot \frac{\sqrt{2}}{2}u_2 \end{cases} \end{eqnarray} \)

Do otrzymanych równań dopisujemy jeszcze równania otrzymane z zasady zachowania energii i tak powstaje układ trzech równań z trzema niewiadomymi \(u_1\), \(u_2\) oraz \(\alpha_1\).

Rozwiązaniem tego układu są liczby \(\displaystyle{u_1=\frac{\sqrt{10}}{4}v_1 }\), \(\displaystyle{u_2=\frac{\sqrt{2}}{4}v_1 }\) oraz \(\alpha_1=71,6^{\circ}\).

Rozwiązanie układu równań

\(\begin{eqnarray} \begin{cases} v_1 &=u_1\cos\alpha_1+3\cdot \frac{\sqrt{2}}{2}u_2\\ 0 &=u_1\sin\alpha_1-3\cdot \frac{\sqrt{2}}{2}u_2\\ v_1^2 &=u_1^2+3u_2^2 \end{cases} \end{eqnarray} \)

W powyższym układzie równań, w pierwszym i drugim równaniu są funkcje trygonometryczne, proponuję więc rozwiązanie, w którym wyznaczymy te funkcje:

\(\displaystyle{\cos\alpha=\frac{v_1-\frac{3}{2}\sqrt{2}\,u_2}{u_1} }\)

\(\displaystyle{\sin\alpha=\frac{\frac{3}{2}\sqrt{2}\,u_2}{u_1} }\)

Po podniesieniu do kwadratu tych równań i dodaniu stronami, otrzymujemy:

\(\displaystyle{\cos^2\alpha+\sin^2\alpha=\frac{v_1^2-2\cdot\frac{3}{2}\sqrt{2}v_1u_2+\frac{9}{4}\cdot 2\,u_2^2}{u_1^2}+\frac{\frac{9}{4}\cdot 2\,u_2^2}{u_1^2} }\)

\(\displaystyle{1=\frac{v_1^2-3\sqrt{2}v_1u_2+\frac{18}{2}\,u_2^2}{u_1^2} }\)

\(u_1^2=v_1^2-3\sqrt{2}v_1u_2+9\,u_2^2\)

Po przekształceniu trzeciego równania, wynikającego z zasady zachowania energii, otrzymujemy:

\(u_1^2=v_1^2-3u_2^2\)

Przyrównując dwa ostatnie równania, mamy:

\(v_1^2-3u_2^2=v_1^2-3\sqrt{2}v_1u_2+9\,u_2^2\)

\(12u_2^2-3\sqrt{2}u_2v_1=0\)

\(4u_2=\sqrt{2}v_1\)

\(\displaystyle{u_2=\frac{\sqrt{2}}{4}v_1 }\)
Prędkość \(u_1\) obliczamy następująco:

\(\displaystyle{u_1^2=v_1^2-3\left (\frac{\sqrt{2}}{4}v_1\right )^2 }\)

\(\displaystyle{u_1^2=v_1^2-\frac{3}{8}v_1^2 }\)

\(\displaystyle{u_1=\sqrt{\frac{5}{8}}v }\)

\(\displaystyle{u_1=\frac{\sqrt{10}}{4}v_1 }\)

Teraz obliczamy wartość kąta
\(\displaystyle{\sin\alpha=\frac{\frac{3}{2}\sqrt{2}\,u_2}{u_1} }\)

\(\displaystyle{\sin\alpha=\frac{\frac{3}{2}\sqrt{2}\,\frac{\sqrt{2}}{4}v_1}{\frac{\sqrt{10}}{4}v_1 } }\)

\(\sin\alpha=0,9487\)
Tak więc kąt \(\alpha=71,6^{\circ}\)

Odpowiedź

Końcowa prędkość cząstki pierwszej wynosi \(\displaystyle{u_1=\frac{\sqrt{10}}{4}v_1 }\), drugiej -  \(\displaystyle{u_2=\frac{\sqrt{2}}{4}v_1 }\) oraz kąt odchylenia toru ruchu cząstki pierwszej ma wartość \(\alpha_1=71,6^{\circ}\).