Zadanie 4.4.1.4
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.4. Zasada zachowania pędu
  4. 4.4.1 Nauka
  5. Zadanie 4.4.1.4

 Zadanie 4.4.1.4

Zderzenie niesprężyste
Kloc drewniany o masie \(4\,\mathrm{kg}\) spada z wysokości \(10\,\mathrm{m}\). W połowie wysokości zostaje trafiony poziomo lecącym pociskiem, który wbija się weń niesprężyście. Masa pocisku wynosi \(0,01\,\mathrm{kg}\), a jego prędkość wynosi \(\displaystyle{500\,\mathrm{\frac{m}{s}}}\). Oblicz wartość prędkości kloca w momencie upadku na Ziemię.

 Wskazówka teoretyczna

 Teoria - zasada zachowania pędu
Zasada zachowania pędu.
Pęd zamkniętego układu ciał nie zmienia się z upływem czasu.

\(\displaystyle{\frac{\mathrm{d}\vec{p} }{\mathrm{d} t}=0}\)
czyli \(\vec{p}=const\)

Zasadę te można też zapisać jako:
Suma pędów wszystkich ciał układu w momencie początkowym równa się sumie pędów tych ciał w dowolnym momencie późniejszym.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa drewnianego kloca \(M=4\,\mathrm{kg}\),
- masa pocisku \(m=0,01\,\mathrm{kg}\),
- prędkość pocisku \(\displaystyle{v_1=500\,\mathrm{\frac{m}{s}}}\),
- wysokości, z jakiej spada kloc \(h=10\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- wartość prędkości kloca w momencie upadku na Ziemię \(u\).

Analiza sytuacji

Przy założeniu, że siła oporu działająca na kloc podczas spadku jest zaniedbywanie mała, na kloc działa jedynie pionowo w dół siła ciężkości. Powoduje ona jego ruch jednostajnie przyspieszony. Zderzenie całkowicie niesprężyste zachodzi w kierunku poziomym, w którym nie działa żadna siła zewnętrzna, dlatego do opisu zderzenia możemy zastosować zasadę zachowania poziomej składowej pędu układu.

Opis matematyczny

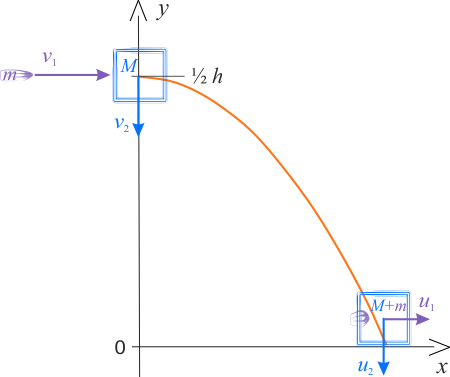
Sytuację w chwili tuż przed trafieniem przez pocisk i w chwili tuż przed spadkiem kloca na Ziemię, z wbitym w kloc pociskiem, przedstawiono na rysunku w dwuwymiarowym układzie współrzędnych \(x\,y\), gdzie oś \(x\) skierowana jest poziomo, zgodnie z kierunkiem ruchu pocisku przed uderzeniem w kloc, a oś \(y\) - pionowo w górę. Na rysunkach prędkości pocisku i kloca oraz składowe pionowe i poziome są reprezentowane przez ich wartości bezwzględne.

Tuż przed zderzeniem pocisk ma, skierowaną poziomo, prędkość \(v_1\), a kloc prędkość \(v_2\), uzyskaną ze swobodnego spadku skierowaną pionowo w dół. Prędkość \(v_2\) możemy otrzymać z zasady zachowania energii. Przyjmując, że na poziomie Ziemi energia potencjalna jest równa zeru, mamy:

\(\displaystyle{Mgh=\frac{Mv_2^2}{2}+Mg\frac{h}{2} }\)

Po zderzaniu kloc z wbitym pociskiem uzyskuje dodatkową prędkość poziomą \(v_1\), którą otrzymamy z zasady zachowania pędu dla kierunku \(x\). Mamy:

\(\sum p_x=mv_1=(M+m)\,u_1\)

\(u_1\) i \(u_2\) są składowymi poziomą i pionowa wektora \(u\).

Rysunek

Rozwiązanie

Z pierwszego równania możemy wyznaczyć prędkość \(v_2\)

\(\displaystyle{gh=\frac{v_2^2}{2}+g\frac{h}{2} }\)
 \[2gh=v_2^2+gh\] \[v_2=\sqrt{gh}\] \[v_2=\sqrt{10\cdot 10}\] \[\displaystyle{\left [ \sqrt{\frac{m}{s^2}\cdot m}=\frac{m}{s} \right ]}\] 
\(\displaystyle{v_2=10\,\mathrm{\frac{m}{s}}}\)

Prędkość \(u_1\) uzyskamy, zaś z równania drugiego

\(\displaystyle{u_1=\frac{mv_1}{M+m}}\) 

\(\displaystyle{u_1=\frac{0,01}{4+0,01}\cdot 500 }\)  \(\displaystyle{\left [ \frac{kg}{kg}\cdot \frac{m}{s}=\frac{m}{s} \right ] }\)

\(\displaystyle{u_1=1,25\,\mathrm{\frac{m}{s}}}\)

Ponieważ po zderzeniu na kloc nie działają żadne siły poziome, uzyskana prędkość pozioma pozostaje stała. Końcową prędkość \(u\) kloca z wbitym pociskiem uzyskamy, stosując zasadę zachowania energii dla klocka z pociskiem. Mamy:

\(\displaystyle{\frac{(M+m)(v_2^2+u_1^2)}{2}+(M+m)\,g\,\frac{h}{2}=\frac{(M+m)u^2}{2} }\)

Po przemnożeniu przez \(\displaystyle{\frac{2}{M+m}}\) otrzymujemy

\(v_2^2+u_1^2+gh=u^2\)

\(u=\sqrt{v_2^2+u_1^2+gh}\)

\(u=\sqrt{10^2+1,25^2+10\cdot 10}\)

\(\displaystyle{u=14,2\,\mathrm{\frac{m}{s}}}\)

Odpowiedź

Wartość prędkości kloca w momencie upadku na Ziemię wynosi \(\displaystyle{u=14,2\,\mathrm{\frac{m}{s}}}\).