Analiza sytuacji

Zgodnie z treścią zadania, zderzenie cząstek jest zderzeniem centralnym i niesprężystym. Podczas zderzenia spełniona jest zasada zachowania pędu, natomiast część energii mechanicznej cząstki ulega zamianie na energię wewnętrzną cząstek. Do rozwiązania zadania, stosujemy zasadę zachowania pędu oraz równanie bilansu energii przy uwzględnieniu jej straty podczas zderzenia cząstek. Zasadę zachowania pędu zastosujemy w postaci skalarnej, gdyż zderzenie jest centralne.

Opis matematyczny

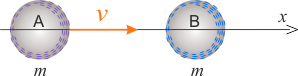
Opis zderzenia cząstek przedstawiono w układzie współrzędnej \(x\), gdzie oś \(x\) jest skierowana zgodnie z początkową prędkością cząstki \(A\)  – w prawo. Sytuację w chwili tuż przed zderzeniem i w chwili tuż po zderzeniu przedstawiono odpowiednio na rysunku a i rysunku b. Oznaczenia prędkości na rysunkach dotyczą ich składowych wzdłuż osi \(x\) (dla uproszczenia nie wprowadzamy dodatkowych oznaczeń tj. \(v_x\) zamiast \(v\), \(u_{1x}\) zamiast \(u_1\) oraz \(u_{2x}\) zamiast \(u_2\)).

Opis matematyczny

Z zasady zachowania pędu (dla kierunku \(x\)) mamy, że:

W równaniu bilansu energii układu cząstek przed i po zderzeniu uwzględniamy, że zgodnie z treścią zadania, \((1-\eta)=91\%\) energii kinetycznej układu zostaje zachowane. Mamy więc:

Rozwiązanie

Otrzymane wyżej równania podzielmy przez \(m\), a otrzymamy:

Ponieważ interesuje nas prędkość pierwszej cząstki \(u_1\), to z pierwszego równania eliminujemy \(u_2\) i po wstawieniu do drugiego otrzymujemy:


Otrzymujemy równanie kwadratowe postaci


 Obliczenia  \[\Delta=4v^2-4\cdot 2\cdot \eta\,v^2=4v^2(1-2\eta)\] \[\displaystyle{u_{11}=\frac{2v-2v\sqrt{(1-2\eta)}}{2\cdot 2}}\] \[\displaystyle{u_{12}=\frac{2v+2v\sqrt{(1-2\eta)}}{2\cdot 2}}\] 
Rozwiązaniem równania są dwie wartości prędkości cząstki \(B\)


Otrzymujemy dwie wartości prędkości \(\displaystyle{u_{11}=0,5\,\mathrm{\frac{m}{s}} }\)  oraz  \(\displaystyle{u_{12}=9,5\,\mathrm{\frac{m}{s}} }\). Jedna z tych wartości nie ma sensu fizycznego. Zobaczmy, jakie prędkości drugiej cząstki odpowiadają poszczególnym rozwiązaniom. Wstawiając \(u_1\) do pierwszego równania otrzymujemy:


Rozwiązanie, w którym prędkość cząstki \(A\) po zderzeniu jest większa od prędkości cząstki \(B\), fizycznie jest niemożliwe, gdyż cząstka \(A\) musiałaby w czasie zderzenia „przeniknąć” przez cząstkę \(B\). Zatem rozwiązaniem zadania są wartości: