Zadanie 4.5.1.5
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.5. Pole grawitacyjne
  4. 4.5.1 Nauka
  5. Zadanie 4.5.1.5

 Zadanie 4.5.1.5

Studnia sięgająca dośrodka Ziemi
Wyobraź sobie, że udało się przewiercić studnię aż do środka Ziemi. Z jaką prędkością upadnie na dno wrzucone do niej ciało? (\(\displaystyle{R_Z=6371\,\mathrm{km},\; g=9,8\,\mathrm{\frac{m}{s^2}}} \)).

 Wskazówka teoretyczna

 Teoria - prawo grawitacji
Prawo grawitacji Newtona.
Jeżeli w przestrzeni umieścimy pewna masę \(M\) (źródło pola grawitacyjnego), to wprowadzając w dowolne miejsce tej przestrzeni inną masę \(m\) w odległości \(r\), stwierdzamy, że na wprowadzoną masę będzie działać siła przyciągania o wartości opisanej prawem grawitacji Newtona:

\(\displaystyle{F=G\frac{Mm}{r^2} }\)

skierowana do źródła pola grawitacyjnego. Współczynnik proporcjonalności \(\displaystyle{G=6,67\cdot 10^{-11}\,\mathrm{\frac{m^3}{kg\,s^2}} }\) nazywamy stałą grawitacji.
Powyższy wzór jest prawdziwy dla mas punktowych i mas kulistosymetrycznych.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- promień Ziemi \(R_Z=6371\,\mathrm{km}\),
- przyspieszenie ziemskie \(\displaystyle{g=9,8\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- prędkość, jaką osiągnie ciało na dnie studni \(v_k\).

Analiza sytuacji

Podczas lotu ciała w dół studni siła grawitacji będzie się zmieniać. Dzieje się tak dlatego, że coraz mniejsza część Ziemi, znajdująca się bliżej środka niż spadające ciało, będzie z nim oddziaływać. Prędkość końcową możemy obliczyć na podstawie pracy siły grawitacyjnej.

Masa Ziemi, która oddziałuje ze spadającym ciałem spełnia zależność

\(\displaystyle{\frac{M'_Z}{M_Z}=\frac{\frac{4}{3}\pi r^3}{\frac{4}{3}\pi R_Z^3}=\frac{r^3}{R_Z^3} }\)

\(\displaystyle{M'_Z=M_Z\frac{r^3}{R_Z^3} }\)

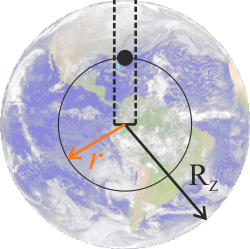
Rysunek


Gdy spadające ciało o masie \(m\) znajduje się w odległości \(r<R_Z\), siła grawitacji wyniesie

\(\displaystyle{F_g=-G\frac{M'_Zm}{r^2} }\)

\(\displaystyle{F_g=-G\frac{M_Zr^3m}{r^2R_Z^3}=-G\frac{M_Z}{R_Z^2}\frac{m}{R_Z}r }\)

\(\displaystyle{F_g=-g\frac{m}{R_Z}r }\)

Pracę siły określa zależność \(\displaystyle{W=\int_{0}^{S}F\,\mathrm{d}S}\), a w naszym przypadku mamy

\(\displaystyle{W=\int_{R_Z}^{0}F_g\,\mathrm{d}r}\)

Rozwiązanie

Po podstawieniu siły grawitacji, mamy

\(\displaystyle{W=-g\frac{m}{R_Z} \int_{R_Z}^{0} r\,\mathrm{d}r=g\frac{m}{R_Z} \int_{0}^{R_Z} r\,\mathrm{d}r }\)

\(\displaystyle{W=g\frac{m}{R_Z}\,\left [ \frac{1}{2}r^2 \right ]_0^{R_Z}=\frac{1}{2}gmR_Z }\)

Teraz z kolei porównajmy wykonaną pracę z energią kinetyczną:

\(\displaystyle{\frac{1}{2}gmR_Z=\frac{1}{2}mv_k^2 }\)

\(v_k=\sqrt{gR_Z} \)

Otrzymana wartość jest równa I prędkości kosmicznej \(v_k=v_I\).

\(\displaystyle{v_k=v_I=7,9\,\mathrm{\frac{km}{s}}}\)

Pierwszą prędkość kosmiczną można wyznaczyć przyrównując siłę odśrodkową, działając na satelitę o masie \(m\) na orbicie kołowej o promieniu zbliżonym do promienia Ziemi \(R_Z\) z siłą przyciągania grawitacyjnego, której źródłem jest Ziemia o masie \(M_Z\).

\(\displaystyle{\frac{mv_I^2}{R_Z}=G\frac{mM_Z}{R_Z^2} }\)

\(R_Z v_I^2=GM_Z \)

\(\displaystyle{\sqrt{\frac{GM_Z}{R_Z}}=\sqrt{\frac{GM_ZR_Z}{R_Z^2}} }\)

\(v_I=\sqrt{gR_Z} \)

\(\displaystyle{v_I=7,9\,\mathrm{\frac{km}{s}}}\)

Odpowiedź

W chwili dotarcia do dna studni, ciało osiągnie prędkość \(\displaystyle{v_k=7,9\,\mathrm{\frac{km}{s}}}\).