Zadanie 5.1.1.5
Środek masy wydrążonej kuli
Znajdź środek masy jednorodnej kuli o promieniu \(r_1=50\,\mathrm{cm}\), w której wnętrzu znajduje się kuliste wydrążenie o promieniu \(r_2=10\,\mathrm{cm}\), przy czym środek kuli mniejszej oddalony jest o \(d=5\,\mathrm{cm}\) od środka kuli większej.
Wskazówka teoretyczna
Teoria - środka masy ciała
Wektor położenia środka masy ciała definiujemy jako
gdzie \(\vec{r}_i^2\) oznacza wektor położenia elementu masy \(\mathrm{d}m\), a \(M\) jest masą całkowitą ciała.
\(\displaystyle{\vec{r}_s=\frac{1}{M}\int_{M} \vec{r}\mathrm{d}m }\),
gdzie \(\vec{r}_i^2\) oznacza wektor położenia elementu masy \(\mathrm{d}m\), a \(M\) jest masą całkowitą ciała.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- promień dużej kuli \(r_1=50\,\mathrm{cm}\),
- promień małej kuli \(r_2=10\,\mathrm{cm}\),
- odległość mniejszej kuli od środka kuli większej \(d=5\,\mathrm{cm}\).
Szukane:
- środek masy kuli wydrążonej \(x_1\).
Analiza sytuacji
Pełna kula o promieniu \(r_1\) składa się z małej kuli o promieniu \(r_2\) i masie \(m_2\) oraz dużej kuli o promieniu \(r_1\) z wydrążeniem i masie \(m_1\).
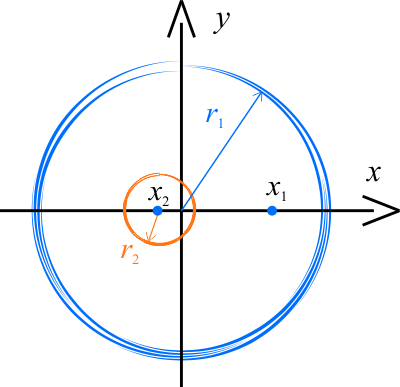
Dla pełnej kuli środek masy ma (w układzie współrzędnych pokazanym na rysunku) współrzędne
\(\displaystyle{x_s=0=\frac{x_1m_1+x_2m_2}{m_1+m_2} }\), \(y_s=0\), \(z_s=0\),
przy czym \(x_1\) oznacza współrzędną środka masy kuli z wydrążeniem, natomiast \(x_2\) oznacza współrzędną środka masy małej kuli, którą usuwamy, tworząc wydrążenie.
Jak widać z rysunku \(x_2=-d\). Z pierwszego równania mamy zatem
\(\displaystyle{0=\frac{x_1m_1-d\,m_2}{m_1+m_2} }\)
\(0=x_1m_1-d\,m_2\)
\(\displaystyle{x_1=\frac{m_2}{m_1}d }\)
Teraz wyznaczmy masę \(m_2\). Zakładamy, że gęstość materiału kuli wynosi \(\rho\), wtedy
\(\displaystyle{m_2=V_2\rho=\frac{4}{3}\pi r_2^3\rho }\)
Masa \(m_1\) równa jest różnicy masy całej pełnej kuli i wydrążenia.
\(\displaystyle{m_1=\frac{4}{3}\pi r_1^3\rho -\frac{4}{3}\pi r_2^3\rho=\frac{4}{3}\pi\rho\left (r_1^3-r_2^3\right ) }\)
Obliczenia
Współrzędna środka masy wynosi
\(\displaystyle{x_1=\frac{m_2}{m_1}d }\)
\(\displaystyle{x_1=\frac{\frac{4}{3}\pi\rho r_2^3}{\frac{4}{3}\pi\rho\left (r_1^3-r_2^3\right )}d }\)
\(\displaystyle{x_1=\frac{r_2^3}{r_1^3-r_2^3}d }\)
\(\displaystyle{x_1=\frac{10^3}{50^3-10^3}\cdot 5 }\)
\(\displaystyle{x_1=\frac{5}{124}\approx0,04\,\mathrm{cm} }\)
\(\displaystyle{x_1=\frac{10^3}{50^3-10^3}\cdot 5 }\)
\(\displaystyle{x_1=\frac{5}{124}\approx0,04\,\mathrm{cm} }\)
Odpowiedź
Współrzędna środka masy wynosi \(\displaystyle{x_1=0,04\,\mathrm{cm} }\).
