Zadanie 5.2.1.1
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 5. Dynamika układu punktów
  3. 5.2. Moment bezwładności
  4. 5.2.1 Nauka
  5. Zadanie 5.2.1.1

 Zadanie 5.2.1.1

Moment bezwładności pręta
Oblicz moment bezwładności jednorodnego pręta o długości \(L\) i masie \(m\) względem osi prostopadłej do pręta i przechodzącej przez:
a) środek pręta,
b) koniec pręta.

 Wskazówka teoretyczna

 Teoria - moment bezwładności
Należy pamiętać o tym, że moment bezwładności ciała \(I\) wyznaczamy zawsze względem pewnej osi. Zmiana osi powoduje zmianę momentu bezwładności.

\(\displaystyle{I=\int_M r_{\perp}^2\,\mathrm{d}m=\int_V r_{\perp}^2\rho\,\mathrm{d}V }\),

gdzie \( r_{\perp}\) - odległość elementu masy \(\mathrm{d}m\) od osi obrotu, \(\rho\) - gęstość ciałą, \(M\) - masa ciała.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- długość pręta \(L\),
- masa pręta \(m\).

Szukane:
- moment bezwładności jednorodnego pręta względem osi prostopadłej do pręta i przechodzącej przez środek pręta \(I_a\),
- moment bezwładności jednorodnego pręta względem osi prostopadłej do pręta i przechodzącej przez koniec pręta \(I_b\).

Analiza sytuacji

Moment bezwładności  Bryłą sztywną nazywamy dowolny zbiór punktów pomiędzy, którymi odległość nie ulega zmianie bez względu na działające siły. Bryłą sztywną możemy nazywać równie dobrze ciało „jednolite” jak i dwa punkty, które są względem siebie nieruchome.   względem zadanej osi obrotu wyznaczymy, licząc następującą całkę:

\(\displaystyle{I=\int_m r^2\,\mathrm{d}m }\),

gdzie \(r\) jest odległością elementu masy \(\mathrm{d}m\) od osi obrotu.

Dla jednorodnego pręta element masy \(\mathrm{d}m=\rho S\mathrm{d}x\), gdzie \(\rho\) jest gęstością pręta, \(S\) polem jego przekroju poprzecznego.

Rozwiązanie - punkt a)

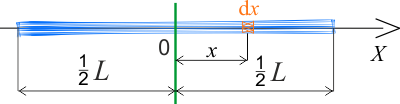
Rysunek


Rysunek ilustruje przypadek, gdy chcemy policzyć moment bezwładności pręta względem osi przechodzącej przez jego środek.

Pamiętając, że w tym przypadku odległość elementu masy od osi obrotu wynosi \(x\), zapisujemy szukany moment bezwładności jako

\(\displaystyle{I_a=\int_{-L/2}^{L/2}x^2\rho S\,\mathrm{d}x }\)
 \[\displaystyle{\int x^n=\frac{1}{n+1}\,x^{n+1}+C,\;\,n\neq -1}\] 
 \[\displaystyle{I_a=\rho S\left [\frac{1}{3}x^3 \right ]_{-L/2}^{L/2} }\] \[\displaystyle{I_a=\rho S\left [\frac{1}{3}\frac{L^3}{2^3}-\frac{1}{3}\frac{(-L)^3}{2^3} \right ] }\] 
\(\displaystyle{I_a=\rho S\frac{L^3}{12} }\)

Całkowita masa pręta wynosi \(m=\rho\,SL\), a stąd mamy \(\displaystyle{\rho\,S=\frac{m}{L} }\). Ostatecznie otrzymujemy

\(\displaystyle{I_a=\frac{1}{12}mL^2 }\)

Rozwiązanie - punkt b)

Wyznaczenie momentu bezwładności pręta względem osi do niego prostopadłej i przechodzącej przez jego koniec, wymaga obliczenia takiej samej całki, jak w pierwszej części zadania, jedynie w innych granicach będzie zmieniać się współczynnik \(x\).

\(\displaystyle{I_b=\int_{0}^{L}x^2\rho S\,\mathrm{d}x }\)

\(\displaystyle{I_b=\frac{1}{3}L^3\rho S }\)

\(\displaystyle{I_b=\frac{1}{3}mL^2 }\)

Odpowiedź

Moment bezwładności jednorodnego pręta względem osi prostopadłej do pręta i przechodzącej przez środek pręta, wynosi \(\displaystyle{I_a=\frac{1}{12}mL^2 }\), zaś osi przechodzącej przez jego koniec, wynosi \(\displaystyle{I_b=\frac{1}{3}mL^2 }\).