Zadanie 5.2.1.2
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.2. Moment bezwładności
  4. 5.2.1 Nauka
  5. Zadanie 5.2.1.2

 Zadanie 5.2.1.2

Momenty bezwładności względem dwóch równoległych osi
Załóżmy, że znamy momenty bezwładności pewnej płaskiej bryły o masie \(m=0,8\,\mathrm{kg}\) względem dwóch równoległych osi leżących w jej (bryły) płaszczyźnie \(I_1=8\,\mathrm{kg\,m^2}\), \(I_2=12\,\mathrm{kg\,m^2}\). Odległość pomiędzy osiami wynosi \(L=1\,\mathrm{m}\). Ile wynosi moment bezwładności dla tej bryły względem osi równoległej do danych, ale przechodzących przez środek masy?

 Wskazówka teoretyczna

 Teoria - twierdzenie Steinera
Twierdzenie Steinera określa związek między momentami bezwładności względem dwóch równoległych osi oddalonych od siebie o \(d\) w sytuacji, gdy jedna z nich przechodzi przez środek masy bryły sztywnej:

\(I=I_0+md^2\),

gdzie \(m\) jest daną masą bryły sztywnej.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa bryły \(m=0,8\,\mathrm{kg}\),
- momenty bezwładności względem pierwszej osi \(I_1=8\,\mathrm{kg\,m^2}\),
- momenty bezwładności względem drugiej osi \(I_2=12\,\mathrm{kg\,m^2}\),
- odległość pomiędzy osiami \(L=1\,\mathrm{m}\).

Szukane:
- moment bezwładności dla tej bryły względem osi równoległej do danych, ale przechodzących przez środek masy \(I_0\).


Analiza sytuacji

Przesuwanie osi obrotu i zmiana momentu bezwładności opisywane jest przez tw. Steinera.
Moment bezwładności \(I_2\), jako większy, powinien znajdować się dalej od środka masy.

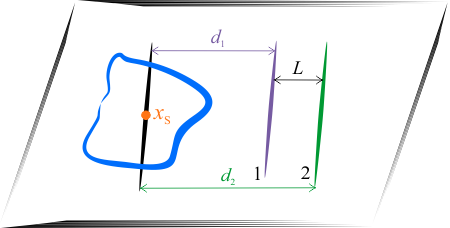
Rysunek


Na podstawie twierdzenia Steinera możemy napisać dwa równania, w których odległość od środka masy osi wyniesie odpowiednio \(d_1\) oraz \(d_2=d_1+L\). Stąd mamy układ dwóch równań

\(I_1=I_0+md_1^2\)

\(I_2=I_0+md_2^2=I_0+m(d_1+L)^2\)

Obliczenia

Rozwiązujemy otrzymany układ równań odejmując od siebie równania stronami. Otrzymujemy

\(I_1-I_2=md_1^2-m(d_1+L)^2\)

Obliczamy teraz z tego równania jedyną niewiadomą  \[I_1-I_2=md_1^2-md_1^2-m2d_1L-mL^2\] \[I_1-I_2=-2md_1L-mL^2\] \[2md_1L=I_2-I_1-mL^2\] 

\(\displaystyle{d_1=\frac{I_2-I_1}{2mL}-\frac{L}{2} }\)

\(\displaystyle{d_1=\frac{12-8}{2\cdot 0,8\cdot 1}-\frac{1}{2} }\)

\(d_1=2\,\mathrm{m}\),

a z jednego z równań np. z pierwszego znajdujemy szukany moment bezwładności bryły względem osi przechodzącej przez środek masy

\(I_0=I_1-md_1^2\)

\(I_0=8-0,8\cdot 2^2\)

\(I_0=4,8\,\mathrm{kg\,m^2}\)

Odpowiedź

Moment bezwładności dla bryły względem osi równoległej do danych, ale przechodzących przez środek masy wynosi \(I_0=4,8\,\mathrm{kg\,m^2}\).