Zadanie 5.2.1.3
Moment bezwładności jednorodnego stożka
Wyznacz moment bezwładności jednorodnego stożka o wysokości \(h\), promieniu podstawy \(r\) i masie \(m\) względem prostej stycznej do podstawy i równoległej do osi symetrii obrotowej stożka.
Wskazówka teoretyczna
Teoria - moment bezwładności
Należy pamiętać o tym, że moment bezwładności ciała \(I\) wyznaczamy zawsze względem pewnej osi. Zmiana osi powoduje zmianę momentu bezwładności.
gdzie \( r_{\perp}\) - odległość elementu masy \(\mathrm{d}m\) od osi obrotu, \(\rho\) - gęstość ciałą, \(M\) - masa ciała.
\(\displaystyle{I=\int_M r_{\perp}^2\,\mathrm{d}m=\int_V r_{\perp}^2\rho\,\mathrm{d}V }\),
gdzie \( r_{\perp}\) - odległość elementu masy \(\mathrm{d}m\) od osi obrotu, \(\rho\) - gęstość ciałą, \(M\) - masa ciała.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- wysokości stożka \(h\),
- promień podstawy stożka \(r\),
- masa stożka \(m\).
Szukane:
- moment bezwładności jednorodnego stożka względem prostej stycznej do podstawy i równoległej do jego osi symetrii obrotowej \(I\).
Analiza sytuacji
Moment bezwładności bryły sztywnej względem zadanej osi obrotu wyznaczymy, licząc następującą całkę:
\(\displaystyle{I=\int_m r^2\,\mathrm{d}m }\),
gdzie \(r\) jest odległością elementu masy \(\mathrm{d}m\) od osi obrotu. Jeżeli bryła sztywna jest jednorodna, to wtenczas element masy \(\mathrm{d}m=\rho\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\), gdzie \(\rho\) jest gęstością bryły, a \(\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\) elementem jej objętości wyrażonym we współrzędnych kartezjańskich. Moment bezwładności jest wtenczas całką potrójną
\(\displaystyle{I=\int_{x_1}^{x_2}\int_{y_1}^{y_2}\int_{z_1}^{z_2} r^2\,\rho\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }\)
Obliczenia momentu bezwładności stożka będą łatwiejsze, jeżeli wprowadzimy współrzędne cylindryczne. W tym przypadku element masy ma postać \(\mathrm{d}m=\rho\,r\,\mathrm{d}r\,\mathrm{d}\varphi\,\mathrm{d}z\).
\(\displaystyle{I=\int_{r_1}^{r_2}\int_{\varphi_1}^{\varphi_2}\int_{z_1}^{z_2} r^3\,\rho\,\mathrm{d}r\,\mathrm{d}\varphi\,\mathrm{d}z }\)
Zadaną bryłę wprowadzimy do powyższego wzoru poprzez odpowiednie zdefiniowanie granic całkowania po każdej ze współrzędnych.
Załóżmy, że liczymy najpierw moment bezwładności \(I_0\) stożka względem jego osi symetrii, następnie zastosujemy twierdzenie Steinera i znajdziemy szukany w zadaniu moment bezwładności.
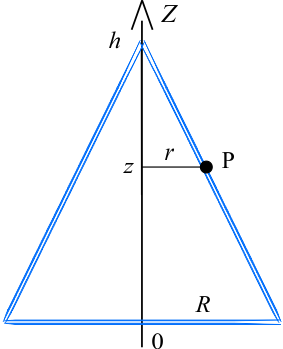
Współrzędna punktu \(z\) to po prostu współrzędna osi obrotu \(0Z\). Współrzędna \(r\) będzie odległością punktu stożka od osi obrotu, natomiast kąt \(\varphi\) jest kątem pomiędzy płaszczyzną rysunku a płaszczyzną, przechodzącą przez oś obrotu i zadany punkt. Wartość tego kąta będzie zmieniać się od \(0\) do \(2\pi\).
Całkowanie po \(\varphi\) da wartość \(2\pi\), ponieważ wyrażenie podcałkowe nie zależy od tego kąta.
\(\displaystyle{I=\int_{z_1}^{z_2}\,\mathrm{d}z \int_{r_1}^{r_2} 2\pi\rho r^3\,\mathrm{d}r }\)
\(\displaystyle{\frac{r}{h-z}=\frac{R}{h} }\)
\(\displaystyle{r=\frac{R}{h}(h-z) }\)
Powyższy związek umożliwi wyznaczenie granic całkowania:\(\displaystyle{r_2(z)=\frac{R}{h}(h-z) }\) oraz \(r_1(z)=0\).
Granice całkowania dla \(z\) to \(z_1=0\) i \(z_2=h\).
Obliczenia
Obliczamy całkę
\(\displaystyle{I_0=\int_{0}^{h}\,\mathrm{d}z \int_{0}^{\frac{R}{h}(h-z)} 2\pi\rho r^3\,\mathrm{d}r }\)
\[\displaystyle{I_0=2\pi\rho\frac{1}{4}\int_{0}^{h}\,\mathrm{d}z \,\left [ r^4\right ]_0^{\frac{R}{h}(h-z)} }\] \[\displaystyle{I_0=\frac{1}{2}\pi\rho\int_{0}^{h} \frac{R^4}{h^4}(h-z)^4\,\mathrm{d}z }\]
\(\displaystyle{I_0=\frac{1}{2}\pi\rho \frac{R^4}{h^4} \int_{0}^{h}(h-z)^4\,\mathrm{d}z }\)
Całkę \(\displaystyle{\int_{0}^{h}(h-z)^4\,\mathrm{d}z }\) można obliczyć przez podstawienie zmiennej \(u=h-z\) oraz \(\mathrm{d}u=-\mathrm{d}z\). Granic całkowania wynoszą \(u=h-0=h\) oraz \(u=h-h=0\). Teraz należy obliczyć następującą całkę
\(\displaystyle{-\int_{h}^{0}(u)^4\,\mathrm{d}u=-\left [ \frac{1}{5}u^5\right ]_h^0=\frac{1}{5}h^5 }\)
\(\displaystyle{I_0=\frac{1}{2}\pi\rho \frac{R^4}{h^4} \cdot \frac{1}{5}h^5 }\)
Moment bezwładności stożka względem jego osi symetrii wynosi:
\(\displaystyle{I_0=\frac{1}{10}\pi\rho R^4h }\)
Masa jednorodnego stożka o gęstości \(\rho\) i objętości \(V\) ma postać:
\(\displaystyle{M=V\rho=\frac{1}{3}\pi r^2h\rho}\)
Moment bezwładności stożka względem jego osi symetrii możemy zapisać jako
\(\displaystyle{I_0=\frac{1}{10}\pi\rho h R^2\cdot R^2=\frac{1}{10}\cdot 3MR^2 }\)
\(\displaystyle{I_0=\frac{3}{10}MR^2 }\)
Moment bezwładności stożka względem osi stycznej do podstawy stożka i równoległej do jego osi symetrii wyznaczamy z twierdzenia Steinera
\(I=I_0+Md^2\)
\(I=\frac{3}{10}MR^2+Md^2\)
\(I=\frac{13}{10}MR^2\)
Odpowiedź
Moment bezwładności stożka względem osi stycznej do podstawy stożka i równoległej do jego osi symetrii wynosi \(I=\frac{13}{10}MR^2\).
