Zadanie 5.2.1.4
Moment bezwładności prostopadłościanu
Znajdź moment bezwładności dla prostopadłościanu o bokach \(a\), \(b\) i \(c\) względem osi przechodzących przez środki przeciwległych ścian.
Wskazówka teoretyczna
Teoria - moment bezwładności
Należy pamiętać o tym, że moment bezwładności ciała \(I\) wyznaczamy zawsze względem pewnej osi. Zmiana osi powoduje zmianę momentu bezwładności.
gdzie \( r_{\perp}\) - odległość elementu masy \(\mathrm{d}m\) od osi obrotu, \(\rho\) - gęstość ciałą, \(M\) - masa ciała.
\(\displaystyle{I=\int_M r_{\perp}^2\,\mathrm{d}m=\int_V r_{\perp}^2\rho\,\mathrm{d}V }\),
gdzie \( r_{\perp}\) - odległość elementu masy \(\mathrm{d}m\) od osi obrotu, \(\rho\) - gęstość ciałą, \(M\) - masa ciała.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- długości boków prostopadłościanu \(a\), \(b\) oraz \(c\).
Szukane:
- momenty bezwładności wyznaczone względem osi przechodzących przez środki przeciwległych ścian \(I_x\), \(I_y\) oraz \(I_z\).
Rozwiązanie
Wybieramy układ współrzędnych tak, aby jego środek leżał w środku prostopadłościanu, a osie \(x\), \(y\) oraz \(z\) przechodziły przez środki ścian.
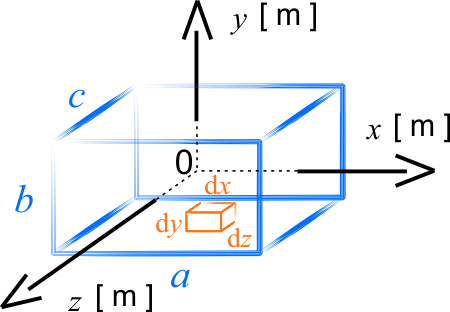
Wyznaczmy moment bezwładności prostopadłościanu względem osi \(x\).
Wewnątrz prostopadłościanu wybieramy mały prostopadłościan o bokach \(\mathrm{d}x\), \(\mathrm{d}y\), \(\mathrm{d}z\). Jego objętość wynosi \(\mathrm{d}V=\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\), a masa \(\mathrm{d}m=\rho \mathrm{d}V\), gdzie \(\rho\) jest gęstością prostopadłościanu. Jest on odległy od osi \(x\) o \(r\), które wynosi
\(r=\sqrt{y^2+z^2}\)
Aby policzyć moment bezwładności prostopadłościanu względem osi \(x\), należy skorzystać z definicji \(\displaystyle{I=\int_M r^2\,\mathrm{d}m}\).
Podstawiając \(r\) i \(\mathrm{d}m\) otrzymujemy całkę
\(\displaystyle{I_x=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( y^2+z^2 \right )\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }\)
Granice całkowania wynikają z obranego układu współrzędnych i długości ścian prostopadłościanu. Całkując najpierw po zmiennej \(x\), otrzymujemy:
\(\displaystyle{I_x=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\left ( y^2+z^2 \right )\,\left [ x\right ]^{\frac{a}{2}}_{-\frac{a}{2}}\mathrm{d}y\,\mathrm{d}z }\)
\(\displaystyle{I_x=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\left ( y^2+z^2 \right )\,a\,\mathrm{d}y\,\mathrm{d}z }\)
Wykonujemy całkowanie po zmiennej \(y\):
\(\displaystyle{I_x=a\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left [ \frac{1}{3}y^3+z^2y \right ]^{\frac{b}{2}}_{-\frac{b}{2}}\,\mathrm{d}z }\)
\[\displaystyle{I_x=a\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left [ \frac{1}{3}\frac{b^3}{2^3}+z^2\frac{b}{2}-\left (-\frac{1}{3}\frac{b^3}{2^3}-z^2\frac{b}{2}\right ) \right ]\,\mathrm{d}z }\] \[\displaystyle{I_x=a\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left ( \frac{1}{3}\frac{b^3}{8}+z^2\frac{b}{2}+\frac{1}{3}\frac{b^3}{8}+z^2\frac{b}{2}\right )\,\mathrm{d}z }\] \[\displaystyle{I_x=a\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left ( \frac{2}{3}\frac{b^3}{8}+z^2b \right )\,\mathrm{d}z }\]
\(\displaystyle{I_x=a\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left ( \frac{b^3}{12}+z^2b \right )\,\mathrm{d}z }\)
Pozostało całkowanie po zmiennej \(z\):
\(\displaystyle{I_x=a\,\rho \left [ \frac{b^3}{12}z+\frac{1}{3}z^3b \right ]^{\frac{c}{2}}_{-\frac{c}{2}} }\)
\(\displaystyle{I_x=a\,\rho \left ( \frac{1}{12}b^3c+\frac{1}{12}c^3b \right ) }\)
\(\displaystyle{I_x=\frac{1}{12}abc\,\rho \left ( b^2+c^2 \right ) }\)
Objętość prostopadłościanu wynosi \(V=abc\), a jego masa \(m=\rho V\), zatem moment bezwładności względem osi \(x\) wynosi
\(\displaystyle{I_x=\frac{1}{12}m \left ( b^2+c^2 \right ) }\)
Analogicznie obliczamy momenty bezwładności względem osi \(y\) oraz \(z\).
Moment bezwładności \(I_y\) liczony względem osi \(y\):
\(\displaystyle{I_y=\frac{1}{12}m \left ( a^2+c^2 \right ) }\)
\(\displaystyle{I_y=\frac{1}{12}m \left ( a^2+c^2 \right ) }\)
Obliczenia \(I_y\)
Odległość małego prostopadłościanu od osi \(y\) wynosi:
\(r_y=\sqrt{x^2+z^2}\)
Moment bezwładności względem tej osi obliczamy z całki
\(\displaystyle{I_y=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+z^2 \right )\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }\)
\(r_y=\sqrt{x^2+z^2}\)
Moment bezwładności względem tej osi obliczamy z całki
\(\displaystyle{I_y=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+z^2 \right )\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }\)
Całkując najpierw po zmiennej \(y\), otrzymujemy:
Wykonujemy całkowanie po zmiennej \(x\):
Pozostało całkowanie po zmiennej \(z\):
Objętość prostopadłościanu wynosi \(V=abc\), a jego masa \(m=\rho V\), zatem moment bezwładności względem osi \(y\) wynosi
\(\displaystyle{I_y=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+z^2 \right )\,\left [ y\right ]^{\frac{b}{2}}_{-\frac{b}{2}}\mathrm{d}x\,\mathrm{d}z }\)
\(\displaystyle{I_y=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+z^2 \right )\,b\,\mathrm{d}x\,\mathrm{d}z }\)
Wykonujemy całkowanie po zmiennej \(x\):
\(\displaystyle{I_y=b\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left [ \frac{1}{3}x^3+z^2x \right ]^{\frac{a}{2}}_{-\frac{a}{2}}\,\mathrm{d}z }\)
\(\displaystyle{I_y=b\,\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}} \left ( \frac{a^3}{12}+z^2a \right )\,\mathrm{d}z }\)
Pozostało całkowanie po zmiennej \(z\):
\(\displaystyle{I_y=ab\,\rho \left [ \frac{a^2}{12}z+\frac{1}{3}z^3 \right ]^{\frac{c}{2}}_{-\frac{c}{2}} }\)
\(\displaystyle{I_y=ab\,\rho \left ( \frac{1}{12}a^2c+\frac{1}{12}c^3 \right ) }\)
\(\displaystyle{I_y=\frac{1}{12}abc\,\rho \left ( a^2+c^2 \right ) }\)
Objętość prostopadłościanu wynosi \(V=abc\), a jego masa \(m=\rho V\), zatem moment bezwładności względem osi \(y\) wynosi
\(\displaystyle{I_y=\frac{1}{12}m \left ( a^2+c^2 \right ) }\)
Moment bezwładności \(I_z\) liczony względem osi \(z\):
\(\displaystyle{I_z=\frac{1}{12}m \left ( a^2+b^2 \right ) }\)
\(\displaystyle{I_z=\frac{1}{12}m \left ( a^2+b^2 \right ) }\)
Obliczenia \(I_z\)
Odległość małego prostopadłościanu od osi \(z\) wynosi:
\(r_z=\sqrt{x^2+y^2}\)
Moment bezwładności względem tej osi obliczamy z całki
\(\displaystyle{I_z=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+y^2 \right )\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }\)
\(r_z=\sqrt{x^2+y^2}\)
Moment bezwładności względem tej osi obliczamy z całki
\(\displaystyle{I_z=\rho\int ^{\frac{c}{2}}_{-\frac{c}{2}}\int^{\frac{b}{2}}_{-\frac{b}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+y^2 \right )\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }\)
Całkując najpierw po zmiennej \(z\), otrzymujemy:
Wykonujemy całkowanie po zmiennej \(x\):
Pozostało całkowanie po zmiennej \(y\):
Objętość prostopadłościanu wynosi \(V=abc\), a jego masa \(m=\rho V\), zatem moment bezwładności względem osi \(z\) wynosi
\(\displaystyle{I_z=\rho\int ^{\frac{b}{2}}_{-\frac{c}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+y^2 \right )\,\left [ z\right ]^{\frac{c}{2}}_{-\frac{c}{2}}\mathrm{d}x\,\mathrm{d}y }\)
\(\displaystyle{I_z=\rho\int ^{\frac{b}{2}}_{-\frac{c}{2}}\int^{\frac{a}{2}}_{-\frac{a}{2}}\left ( x^2+y^2 \right )\,c\,\mathrm{d}x\,\mathrm{d}y }\)
Wykonujemy całkowanie po zmiennej \(x\):
\(\displaystyle{I_z=c\,\rho\int ^{\frac{b}{2}}_{-\frac{b}{2}} \left [ \frac{1}{3}x^3+y^2x \right ]^{\frac{a}{2}}_{-\frac{a}{2}}\,\mathrm{d}y }\)
\(\displaystyle{I_z=c\,\rho\int ^{\frac{b}{2}}_{-\frac{b}{2}} \left ( \frac{a^3}{12}+y^2a \right )\,\mathrm{d}y }\)
Pozostało całkowanie po zmiennej \(y\):
\(\displaystyle{I_z=ac\,\rho \left [ \frac{a^2}{12}y+\frac{1}{3}y^3 \right ]^{\frac{b}{2}}_{-\frac{b}{2}} }\)
\(\displaystyle{I_z=ac\,\rho \left ( \frac{1}{12}a^2b+\frac{1}{12}b^3 \right ) }\)
\(\displaystyle{I_z=\frac{1}{12}abc\,\rho \left ( a^2+b^2 \right ) }\)
Objętość prostopadłościanu wynosi \(V=abc\), a jego masa \(m=\rho V\), zatem moment bezwładności względem osi \(z\) wynosi
\(\displaystyle{I_z=\frac{1}{12}m \left ( a^2+b^2 \right ) }\)
Odpowiedź
Momenty bezwładności wyznaczone względem osi przechodzących przez środki przeciwległych ścian wynoszą:
\(\displaystyle{I_x=\frac{1}{12}m \left ( b^2+c^2 \right ) }\)
\(\displaystyle{I_y=\frac{1}{12}m \left ( a^2+c^2 \right ) }\)
\(\displaystyle{I_z=\frac{1}{12}m \left ( a^2+b^2 \right ) }\)
