Zadanie 5.2.1.5

Moment bezwładności cząsteczki

Oblicz moment bezwładności dla cząsteczki dwutlenku siarki (tlenek siarki (IV))

$\mathrm{SO_2}$ względem osi

$x$ i

$y$ przechodzących przez środek ciężkości. Długość wiązania

$\mathrm{SO}$ wynosi

$143\,\mathrm{pm}$ , a kąt

$\mathrm{OSO}$ ma miarę

$119^{\circ}$ .

Wskazówka teoretyczna

Teoria - środek masy, moment bezwładności

Wektor położenia środka masy układu

$N$ punktów materialnych definiujemy jako

$\displaystyle{\vec{r}_s=\frac{1}{M}\sum_{i=1}^{N}m_i \vec{r}_i^2 }$ ,

gdzie

$m_i$ i

$\vec{r}_i^2$ to odpowiednio masa i wektor położenia i-tego punktu materialnego, a

$M$ jest masą całego układu.

Jeżeli bryłę sztywną potraktujemy jako układ

$N$ punktów materialnych, to moment bezwładności takiego układu możemy wyznaczyć z następującego wzoru:

$\sum_{i=1}^N m_i r_1^2$ ,

gdzie

$m_i$ jest masą i-tego punktu materialnego, a

$r_i$ jego odległością od osi obrotu. Wyrażenie

$m_i r_1^2$ jest momentem bezwładności tego punktu materialnego względem zadanej osi obrotu. Powyższy wzór możemy zastosować również dla układu

$N$ ciał o małych rozmiarach liniowych, połączonych na sztywno.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- długość wiązania $\mathrm{SO}$ : $a=143\cdot 10^{-12}\,\mathrm{m}$ ,
- kąt $\mathrm{OSO}$ : $\alpha=119^{\circ}$ .

Szukane:
- momenty bezwładności liczone względem osi $x$ i $y$ przechodzących przez środek ciężkości cząsteczki: $I_x$ , $I_y$ .

Rozwiązanie

W pierwszej kolejności należy wyznaczyć środek bezwładności cząsteczki. Masa atomowa siarki, odczytana układu okresowego, wynosi $32\mathrm{u}$ , a tlenu $16\mathrm{u}$ . Umieśćmy teraz cząsteczkę w układzie współrzędnych, tak jak pokazano na poniższym rysunku.

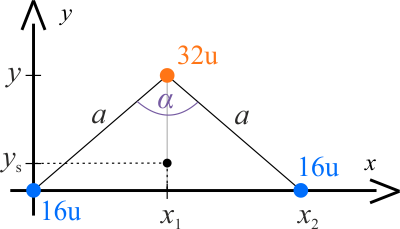
W obranym układzie współrzędnych położenia atomów cząsteczki są następujące

$(0,0)$ ,

$(x_2,0)$ ,

$(x_1,y)$ .

Z rysunku wynika, że

$\displaystyle{\sin{\frac{\alpha}{2}}=\frac{x_1}{a} }$ oraz

$\displaystyle{\cos{\frac{\alpha}{2}}=\frac{y}{a} }$

$\displaystyle{x_1=a\,\sin{\frac{\alpha}{2}} }$ oraz

$\displaystyle{y=a\,\cos{\frac{\alpha}{2}} }$

Mając położenia atomów cząsteczki, możemy wyznaczyć położenie środka masy. Zacznijmu od współrzędnej

$x_s$ .

$\displaystyle{x_s=\frac{16\mathrm{u}\cdot 0+16\mathrm{u}\cdot x_2+32\mathrm{u}\cdot x_1}{16\mathrm{u}+16\mathrm{u}+32\mathrm{u}}}$

$\displaystyle{x_s=\frac{\mathrm{u}(16\cdot 2a\,\sin{\frac{\alpha}{2}}+32\cdot a\,\sin{\frac{\alpha}{2}})}{\mathrm{u}64}}$

$\displaystyle{x_s=a\,\sin{\frac{\alpha}{2}} }$

Współrzędna

$x_s=x_1$

Dla współrzędnej

$y_s$ mamy:

$\displaystyle{y_s=\frac{16\mathrm{u}\cdot 0+16\mathrm{u}\cdot 0+32\mathrm{u}\cdot y}{16\mathrm{u}+16\mathrm{u}+32\mathrm{u}}}$

$\displaystyle{y_s=\frac{32\cdot a\,\cos{\frac{\alpha}{2}}}{64}}$

$\displaystyle{y_s=\frac{a}{2}\,\cos{\frac{\alpha}{2}} }$

Wektor położenia środka masy wynosi

$\displaystyle{r_s=(a\,\sin{\frac{\alpha}{2}},\frac{a}{2}\,\cos{\frac{\alpha}{2}}) }$ .

Moment bezwładności mamy policzyć względem osi przechodzących przez środek ciężkości. Zaznaczmy zatem osie przechodzące przez ten punkt.

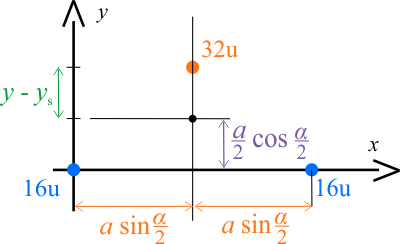
Odległość

$y-y_s$ wynosi

$\displaystyle{y-y_s=a\,\cos{\frac{\alpha}{2}}-\frac{a}{2}\,\cos{\frac{\alpha}{2}}=\frac{a}{2}\,\cos{\frac{\alpha}{2}} }$

Moment bezwładności względem osi poziomej przechodzącej przez środek ciężkości wynosi:

$\displaystyle{I_x=2\cdot 16\mathrm{u}\cdot \left (\frac{a}{2}\cos \frac{\alpha}{2}\right )^2+32\mathrm{u}\cdot \left (\frac{a}{2}\cos \frac{\alpha}{2}\right )^2 }$

$\displaystyle{I_x=64\mathrm{u}\,\frac{a^2}{4}\cos^2\frac{\alpha}{2} }$

$\displaystyle{I_x=16\mathrm{u}\,a^2\cos^2\frac{\alpha}{2} }$

$\displaystyle{I_x=16\cdot 1,66\cdot 10^{-27}\cdot (143\cdot 10^{-12})^2\cdot \cos^2\frac{119}{2} }$

$\displaystyle{I_x=1,4\cdot 10^{-46}\;\mathrm{kg\cdot m^2} }$

Moment bezwładności względem osi pionowej przechodzącej przez środek ciężkości wynosi:

$\displaystyle{I_y=2\cdot 16\mathrm{u}\cdot \left (a\sin \frac{\alpha}{2}\right )^2 }$

$\displaystyle{I_y=32\cdot 1,66\cdot 10^{-27}\cdot (143\cdot 10^{-12})^2\cdot \sin^2\frac{119^{\circ}}{2} }$

$\displaystyle{I_y=8,1\cdot 10^{-46}\;\mathrm{kg\cdot m^2} }$

Odpowiedź

Moment bezwładności dla cząsteczki dwutlenku siarki względem osi przechodzących przez środek ciężkości wynoszą:

$\displaystyle{I_x=1,4\cdot 10^{-46}\;\mathrm{kg\cdot m^2} }$

$\displaystyle{I_y=8,1\cdot 10^{-46}\;\mathrm{kg\cdot m^2} }$

Zadanie 5.2.1.4

Zadanie 5.2.1.6

Wstęp

1. Wektory

2. Kinematyka

3. Zasady dynamiki

4. Praca, moc, energia, pęd

5. Dynamika układu punktów

6. Drgania i fale

7. Elektryczność

Ankieta