Zadanie 5.2.1.6
a) Oblicz składowe tensora bezwładności względem osi \(x\), \(y\) i \(z\).
b) Sprowadź ten tensor na osie główne.
Wskazówka teoretyczna
\(I_{xx}=\sum_{N}^{i=1}m_i\left ( y_i^2+z_i^2 \right )\), \(I_{xy}=-\sum_{N}^{i=1}m_ix_iy_i\),
\(I_{yy}=\sum_{N}^{i=1}m_i\left ( x_i^2+z_i^2 \right )\), \(I_{xz}=-\sum_{N}^{i=1}m_ix_iz_i\),
\(I_{zz}=\sum_{N}^{i=1}m_i\left ( x_i^2+y_i^2 \right )\), \(I_{yz}=-\sum_{N}^{i=1}m_iy_iz_i\)
i można je zapisać w postaci macierzy
\(\hat{I}=\begin{bmatrix}
I_{xx} &I_{xy} &I_{xz} \\
I_{xy} &I_{yy} &I_{yz} \\
I_{xz} &I_{yz} &I_{zz}
\end{bmatrix}\)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
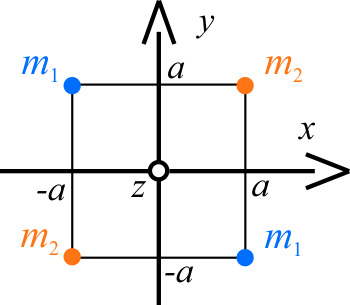
Dane:
- bok kwadratu \(2a\),
- cztery masy \(m_1\), \(m_2\), \(m_1\), \(m_2\).
Szukane:
- składowe tensora bezwładności \(\hat{I}\).
Rozwiązanie - punkt a)
Składowe tensora bezwładności względem osi \(x\), \(y\) oraz \(z\) obliczamy ze wzorów, w których sumowanie przebiega po wszystkich \(N\) punktach układu. W naszym przypadku \(N=4\), a odpowiednie składowe tensora wynoszą:
\(I_{xx}=\sum_{4}^{i=1}m_i\left ( y_i^2+z_i^2 \right )\), \(I_{yy}=\sum_{4}^{i=1}m_i\left ( x_i^2+z_i^2 \right )\)
\[I_{xx}=m_1(a^2+0^2)+m_2(a^2+0^2)+m_1((-a)^2+0^2)+m_2((-a)^2+0^2) \] \[I_{xx}=m_1 a^2+m_2 a^2+m_1 a^2+m_2 a^2 \] \[I_{xx}=2m_1 a^2+2m_2 a^2 \]
\[I_{zz}=m_1\left ( (-a)^2+a^2\right )+m_2\left ( a^2+a^2\right )+m_1\left ( a^2+(-a)^2\right )+m_1\left ( (-a)^2+(-a)^2\right ) \] \[I_{zz}=m_1 2a^2+m_2 2a^2+m_1 2a^2+m_2 2a^2 \] \[I_{zz}=4a^2 (m_1+m_2) \]
\[I_{xy}=-\left [m_2aa+m_1(-a)a+m_2(-a)(-a)+m_1a(-a) \right ] \] \[I_{xy}=-\left [m_2a^2-m_1a^2+m_2a^2-m_1a^2 \right ] \] \[I_{xy}=-\left [-2m_1a^2+2m_2a^2 \right ] \]
Rozwiązanie - punkt b)
Jeżeli, dla uproszczenia zapisu, wprowadzimy następujące oznaczenia:
to tensor bezwładności możemy zapisać jako:
Sprowadzenie tensora na osie główne, oznacza znalezienie takiego nowego układu współrzędnych, w którym tensor bezwładności ma tylko dwie składowe diagonalne. Naszym zadaniem jest znalezienie tych składowych, jak również określenie położenia osi nowego układu współrzędnych w starym układzie.
Oznaczmy osie nowego układu współrzędnych jako \(1\), \(2\), \(3\), a momenty bezwładności względem nich (składowe diagonalne), jako \(I_1\), \(I_2\), \(I_3\). Załóżmy teraz, że nasz układ obraca się względem którejś z osi głównych z pewną prędkością kątową \(\vec{\omega}\) i napiszmy wyrażenie na moment pędu bryły sztywnej \(\vec{L}\).
gdzie \(\omega_x\), \(\omega_y\), \(\omega_z\) są składowymi momentu pędu w starym układzie współrzędnych. Z drugiej strony, jeżeli obrót układu zachodzi dookoła którejś z osi głównych, to kierunek momentu pędu jest taki sam jak wektora prędkości kątowej i wynosi \(\vec{L}=I\,\vec{\omega}\), gdzie \(I\) jest momentem bezwładności względem tej osi. Jeżeli teraz porównamy obydwa wyrażenia na \(\vec{L}\), to otrzymujemy:
Otrzymane równanie jest równoważne układowy trzech równań jednorodnych z niewiadomymi \(\omega_x\), \(\omega_y\), \(\omega_z\). Układ ten ma niezerowe rozwiązanie tylko wtedy, gdy wyznacznik główny tego układu równy jest zeru.
\[(A-I)(A-I)(2A-I)-B\cdot 0\cdot 0+0\cdot B\cdot 0-(A-I)\cdot 0\cdot 0-B\cdot B\cdot (2A-I)-0\cdot (A-I)\cdot 0=0\] \[(A-I)^2(2A-I)-B^2(2A-I)=0\] \[(2A-I)\left [(A-I)^2-B^2\right ]=0\]
Otrzymane równanie daje trzy rozwiązania:
Uzyskane rozwiązania są wartościami głównych momentów bezwładności naszego układu. W zasadzie już z ich postaci możemy wywnioskować, że układ osi nowego układu współrzędnych jest taki jak na rysunku poniżej.
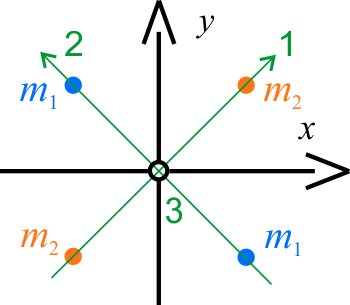
W sposób formalny kierunki osi głównych znajdujemy rozwiązując układ równań na składowe wektora prędkości kątowej \(\vec{\omega}\) skierowanej wzdłuż jednej z trzech osi głównej, odpowiadającej zadanemu głównemu momentowi bezwładności \(I\).
Ponieważ jest to układ równań jednorodnych to tylko dwa równania są liniowo niezależne. Dla \(I=I_1=A+B\) mamy:
Stąd wynika, że \(\omega_x=\omega_y\) oraz \(\omega_z=0\), co interpretujemy w ten sposób, że oś \(1\) jest w płaszczyźnie \(XY\) pod kątem \(45^{\circ}\) w stosunku do osi \(x\) i \(y\). Podobnie, gdy \(I=I_2=A-B\) mamy \(\omega_y=-\omega_x\) oraz \(\omega_z=0\) (oś \(2\) na rysunku), natomiast dla \(I=I_3=2A\) układ równań ma postać:
Dwa pierwsze równania są niesprzeczne jedynie, gdy \(\omega_x=\omega_y=0\), natomiast w trzecim mamy zawsze tożsamość. Stąd wnioskujemy, że wektor \(\vec{\omega}\), skierowany wzdłuż osi głównej \(3\), ma tylko składową \(z\), czyli oś \(3\) pokrywa się z tą osią.
Odpowiedź
Tensor bezwładności względem ma postać:
