Zadanie 5.2.2.1
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- podstawa trójkąta \(a\),
- wysokość trójkąta \(h\),
- gęstość powierzchniowa \(\sigma\).
Szukane:
- moment bezwładności względem podstawy jako osi \(I\).
Odpowiedź
Moment bezwładności trójkąta względem podstawy jako osi wynosi \(\displaystyle{I=\frac{1}{12}\sigma\,ah^3 }\).
Polecenie
Wyznacz moment bezwładności trójkąta. Wybierz jedno prawidłowe rozwiązanie, spośród czterech przedstawionych poniżej.
\(\displaystyle{I=\frac{1}{6}\sigma ah }\)
\(\displaystyle{I=\frac{1}{12}\sigma ah^2 }\)
Rozwiązanie
Dany trójkąt dzielimy na bardzo wąskie paski i rozpatrujemy dowolny pasek o długości \(b\) i grubości \(\mathrm{d}x\), odległy od podstawy trójkąta o \(x\).
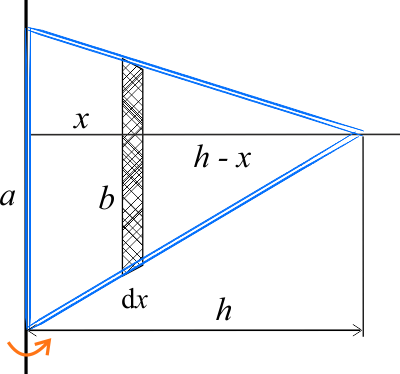
Masa kawałka trójkąta wynosi \(\mathrm{d}m=\sigma\,\mathrm{d}S=\sigma b\,\mathrm{d}x \). Z rysunku wynika, że
Masę kawałka trójkąta możemy zapisać:
Moment bezwładności trójkąta to całka
Po podstawieniu \(\mathrm{d}m\), mamy:
\[\displaystyle{I=\sigma\,a\int_0^h \left (x^2-\frac{x^3}{h}\right )\,\mathrm{d}x }\] \[\displaystyle{I=\sigma\,a\left [\frac{1}{3}x^3-\frac{x^4}{4h}\right ]_0^h }\]
Odpowiedź
Moment bezwładności trójkąta względem podstawy jako osi wynosi \(\displaystyle{I=\frac{1}{12}\sigma\,ah^3 }\).
