Zadanie 5.3.1.1
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.3. Ruch obrotowy bryły sztywnej
  4. 5.3.1 Nauka
  5. Zadanie 5.3.1.1

 Zadanie 5.3.1.1

Krążek i dwie masy
Dwa odważniki o masach \(m_1=2\,\mathrm{kg}\), \(m_2=1\,\mathrm{kg}\) są połączone nicią przerzuconą przez krążek. Promień krążka wynosi \(R=0,1\,\mathrm{m}\), a jego masa \(m=1\,\mathrm{kg}\). Oblicz:
a) przyspieszenie, z jakim poruszają się odważniki,
b) naciągi nici, na których zawieszone są odważniki.
Krążek należy uważać za jednorodny, a tarcie pominąć.

 Wskazówka teoretyczna

 Teoria - II zasada dynamiki
Druga zasada dynamiki dla ruchu obrotowego    

\(\vec{M}=I\vec{\varepsilon}\),

gdzie \(\vec{\varepsilon}\) jest przyspieszeniem kątowym, \(I\) momentem bezwładności (równanie prawdziwe dla stałego momentu bezwładności).

\(\vec{M}\mathrm{d}t=\mathrm{d}\vec{L}\)
 
Komentarz: są to odpowiedniki równań dla ruchu postępowego:

\(\vec{F}=m\vec{a}\)

\(\vec{F}\mathrm{d}t=\mathrm{d}\vec{p}\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa pierwszego odważnika \(m_1=2\,\mathrm{kg}\),
- masa drugiego odważnika \(m_2=1\,\mathrm{kg}\),
- promień krążka \(R=0,1\,\mathrm{m}\),
- masa krążka \(m=1\,\mathrm{kg}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- przyspieszenie, z jakim poruszają się odważniki \(a\),
- naciągi nici, na których zawieszone są odważniki \(N\).

Analiza sytuacji

W rozwiązaniu należy zastosować drugą zasadę dynamiki dla ruchu postępowego z przyspieszeniem \(a\) dla każdego z odważników. Trzeba przy tym uwzględnić to, że jeden z odważników będzie opadać, a drugi będzie się wznosić oraz należy także wziąć pod uwagę ruch obrotowy walca z przyspieszeniem kątowym \(\varepsilon\). Załóżmy do celów rachunkowych, że dodatni zwrot mają wektory skierowane pionowo w dół.

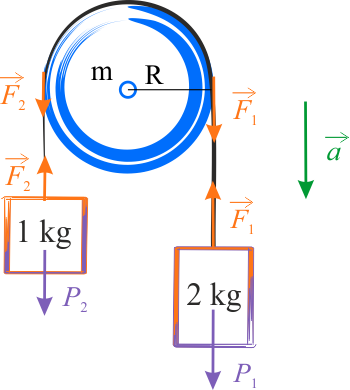
Rysunek

Rozwiązanie

Zgodnie z oznaczeniami z rysunku mamy:

\(m_1a=P_1-F_1\)

\(-m_2a=P_2-F_2\)

\(I\varepsilon =(F_1-F_2)R\)

Nić nie ślizga się po krążku i dlatego zachodzi związek:

\(a=\varepsilon R\)

Potrzebny nam jeszcze będzie wzór określający moment bezwładności krążka względem osi obrotu pokrywającej się z osią symetrii krążka.

\(\displaystyle{I=\frac{1}{2}mR^2 }\)

Ciężar każdego z odważników można wyrazić, korzystając z wartości przyspieszenia ziemskiego \(g\).

\(P_1=m_1g\)

\(P_2=m_2g\)

W ten sposób otrzymujemy układ równań:

\(\begin{eqnarray} \begin{cases} m_1a &=m_1g-F_1 \\ m_2a &=F_2-m_2g \\ \frac{1}{2}mR^2\frac{a}{R} &=(F_1-F_2)R \end{cases} \end{eqnarray} \)

Punkt a)
Wyznaczmy przyspieszenie liniowe \(a\) odważników, rozwiązując otrzymany układ trzech równań

\(\begin{eqnarray} \begin{cases} m_1a &=m_1g-F_1 \\ m_2a &=F_2-m_2g \\ \frac{1}{2}mRa &=(F_1-F_2)R \end{cases} \end{eqnarray} \)

 Dwa pierwsze równania dodajemy stronami. \[\begin{eqnarray} \begin{cases} a(m_1+m_2) =g(m_1-m_2)-(F_1-F_2) \\ \frac{1}{2}ma =F_1-F_2 \end{cases} \end{eqnarray} \] \[\displaystyle{a(m_1+m_2) =g(m_1-m_2)-\frac{1}{2}ma }\] \[\displaystyle{a(m_1+m_2+\frac{1}{2}m) =g(m_1-m_2) }\] \[\displaystyle{a=\frac{g(m_1-m_2)}{m_1+m_2+\frac{1}{2}m} }\] \[\displaystyle{a=\frac{10\,(2-1)}{2+1+\frac{1}{2}} }\] 
\(\displaystyle{a=2,9\,\mathrm{\frac{m}{s^2}} }\)
Punkt b)
Obliczmy siły naciągu nici \(F_1\) i \(F_2\)
\(F_1=m_1(g-a)\)

\(F_1=2\cdot (10-2,9)\)

\(F_1=14,2\,\mathrm{N}\)

Naciąg \(F_2\) wynosi
\(F_2=m_2(g+a)\)

\(F_2=1\cdot (10+2,9)\)

\(F_2=12,9\,\mathrm{N}\)

Odpowiedź

Przyspieszenie, z jakim poruszają się odważniki wynosi \(\displaystyle{a=2,9\,\mathrm{\frac{m}{s^2}} }\), natomiast naciągi nici, na których zawieszone są odważniki, mają wartości \(F_1=14,2\,\mathrm{N}\) oraz \(F_2=12,9\,\mathrm{N}\).