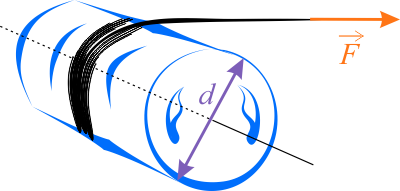
Zadanie 5.3.1.2
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.3. Ruch obrotowy bryły sztywnej
  4. 5.3.1 Nauka
  5. Zadanie 5.3.1.2

 Zadanie 5.3.1.2

Walec ciągnięty za linę
Na walec o średnicy \(0,4\,\mathrm{m}\) i masie \(100\,\mathrm{kg}\) nawinięto długą linę, a następnie przez \(2\,\mathrm{s}\) ciągnięto za nią z siłą \(200\,\mathrm{N}\). Jaką częstość obrotową uzyskał walec?

 Wskazówka teoretyczna

 Teoria - II zasada dynamiki
Druga zasada dynamiki dla ruchu obrotowego    

\(\vec{M}=I\vec{\varepsilon}\),

gdzie \(\vec{\varepsilon}\) jest przyspieszeniem kątowym, \(I\) momentem bezwładności (równanie prawdziwe dla stałego momentu bezwładności).

\(\vec{M}\mathrm{d}t=\mathrm{d}\vec{L}\)
 
Komentarz: są to odpowiedniki równań dla ruchu postępowego:

\(\vec{F}=m\vec{a}\)

\(\vec{F}\mathrm{d}t=\mathrm{d}\vec{p}\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- średnica walca \(d=0,4\,\mathrm{m}\),
- masa walca \(M=100\,\mathrm{kg}\),
- czas ciągnięcia za linę \(t=2\,\mathrm{s}\),
- siła, z jaką ciągnięto za linę \(F=200\,\mathrm{N}\).

Szukane:
- częstotliwość obrotowa, jaką uzyskał walec \(f\).

Analiza sytuacji

Dynamika ruchu obrotowego bryły sztywnej opisywana jest przez wektor momentu pędu. Moment pędu może być zmieniony jedynie przez niezerowy moment siły.

Rysunek

Rozwiązanie

Do obliczenia momentu siły potrzebna jest znajomość  Ramię siły jest najmniejszą odległością między osią obrotu a linią działania kierunku siły.  . Ramię siły w tym przypadku wynosi \(\displaystyle{R=\frac{d}{2}}\). Ponieważ wektory ramienia i siły są do siebie prostopadłe otrzymujemy

\(\displaystyle{M=RF=\frac{d}{2}F}\)
 
Moment bezwładności walca   
\(\displaystyle{I=\frac{1}{2}MR^2=\frac{1}{8}Md^2 }\)

Korzystamy teraz z drugiej zasady dynamiki dla ruchu obrotowego w formie opisującej zmianę momentu pędu

\(\vec{M}\mathrm{d}t=\mathrm{d}\vec{L}\)
 
Ponieważ moment siły jest stały możemy zapisać  
\(Mt=\Delta L\)

Podstawiając wzór na moment siły i dodatkowo korzystając z zależności pomiędzy \(\omega\) i \(f\) (\(\omega=2\pi f\)) otrzymujemy:

\(\displaystyle{\frac{d}{2}Ft=\Delta L=I\omega=\frac{1}{8}Md^2\,2\pi f}\)

\(\displaystyle{\frac{d}{2}Ft=\frac{1}{4}\pi Md^2 f}\)

\(\displaystyle{f=\frac{2Ft}{\pi Md}}\)  \(\displaystyle{\left [ \mathrm{\frac{Ns}{m\,kg}=\frac{kg\cdot m\cdot s}{s^2kg\cdot m}=\frac{1}{s} } \right ]}\)

\(\displaystyle{f=\frac{2\cdot 200\cdot 2}{\pi\cdot 100\cdot 0,4}}\) 

\(\displaystyle{f=\frac{20}{\pi} \approx 6,4\,\mathrm{Hz}}\)

Odpowiedź

Wartość częstotliwości obrotowej, jaką uzyskał walec, wynosi \(\displaystyle{f\approx 6,4\,\mathrm{Hz}}\).