Zadanie 5.3.1.3
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.3. Ruch obrotowy bryły sztywnej
  4. 5.3.1 Nauka
  5. Zadanie 5.3.1.3

 Zadanie 5.3.1.3

Koło Maxwella
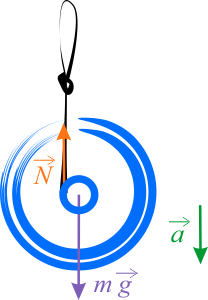
Koło Maxwella to taka trochę bardziej naukowa nazwa popularnej zabawki JoJo. Składa się ono z cienkiej osi, na którą nawinięty jest sznurek i większego koła (kół) o stosunkowo dużym momencie bezwładności. Oblicz, z jakim przyspieszeniem będzie poruszać się swobodnie rozwijające koło Maxwella (JoJo). Przyjmij następujące dane: masa \(200\,\mathrm{g}\), średnica osi \(d=6\,\mathrm{mm}\), moment bezwładności \(I=2,5\cdot 10^{-6}\,\mathrm{kgm^2}\). Załóż, ze sznurek jest cienki a jego masa jest pomijalnie mała. Oblicz siłę naprężenia sznurka.

 Wskazówka teoretyczna

 Teoria - II zasada dynamiki
Druga zasada dynamiki dla ruchu obrotowego    

\(\vec{M}=I\vec{\varepsilon}\),

gdzie \(\vec{\varepsilon}\) jest przyspieszeniem kątowym, \(I\) momentem bezwładności (równanie prawdziwe dla stałego momentu bezwładności).

\(\vec{M}\mathrm{d}t=\mathrm{d}\vec{L}\)
 
Komentarz: są to odpowiedniki równań dla ruchu postępowego:

\(\vec{F}=m\vec{a}\)

\(\vec{F}\mathrm{d}t=\mathrm{d}\vec{p}\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Jeśli chcesz zobaczyć doświadczenie z krążkiem Maxwella, uruchom kliknięciem link  Krążek Maxwella. .

Dane i szukane

Dane:
- masa krążka \(200\,\mathrm{g}=0,2\,\mathrm{kg}\),
- średnica osi \(d=6\,\mathrm{mm}\),
- promień \(r=3\,\mathrm{mm}=0,003\,\mathrm{m}\),
- moment bezwładności \(I=2,5\cdot 10^{-6}\,\mathrm{kgm^2}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- przyspieszenie swobodnie rozwijającego się krążka \(a\),
- siła naprężenia sznurka \(N\).

Analiza sytuacji

Przyspieszenie liniowe \(a\) jest powiązane z przyspieszeniem kątowym koła \(\displaystyle{\varepsilon=\frac{a}{r}}\). Na ruch mają wpływ dwie siły naciągu sznurka \(\vec{N}\) i siła grawitacji \(m\vec{g}\).

Rysunek

Rozwiązanie

Z zasady dynamiki ruchu postępowego otrzymujemy  

\(mg-N=ma\)

Aby skorzystać z zasady dynamiki dla ruchu obrotowego musimy wybrać oś obrotu i policzyć momenty wszystkich sił względem tej osi. Jeżeli za oś obrotu przyjmiemy ośkę naszego koła, wówczas moment siły grawitacji wyniesie zero, natomiast moment siły naciągu wyniesie \(M_N=rN\) i będzie to moment całkowity działających sił. Otrzymujemy wówczas z drugiej zasady dynamiki dla ruchu obrotowego

\(\vec{M}=I\vec{\varepsilon}\)

\(\displaystyle{rN=I\frac{a}{r}}\),

co wraz z poprzednim równaniem daje układ równań, z którego można policzyć zarówno przyspieszenie, jak i siłę naciągu.

\(\begin{eqnarray} \begin{cases} r^2N &=Ia\\ mg-N &=ma \end{cases} \end{eqnarray} \)
 \[\begin{eqnarray} \begin{cases} Ia &=r^2mg-r^2ma\\ N &=mg-ma \end{cases} \end{eqnarray} \] \[r^2mg=a(I+mr^2)\] \[\displaystyle{a=\frac{r^2mg}{I+mr^2}}\] \[\displaystyle{a=\frac{mg}{\frac{I}{r^2}+m}}\] 
\(\displaystyle{a=\frac{0,2\cdot 10}{\frac{2,5\cdot 10^{-6}}{0,003^2}+0,2}\approx 4,2 }\)  

\(\displaystyle{\mathrm{\left [ \frac{kg\cdot \frac{m}{s^2}}{\frac{kg\,m^2}{m^2}+kg}=\frac{kg\frac{m}{s^2}}{kg}=\frac{m}{s^2} \right ]} }\)

\(N=0,2\cdot 10-0,2\cdot 4,2=1,16\,\mathrm{N}\)

Obliczone przyspieszenie wyniesie \(\displaystyle{a\approx 4,2\,\mathrm{\frac{m}{s^2}}}\)  siła naciągu \(N=1,16\,\mathrm{N}\).

Odpowiedź

Obliczone przyspieszenie wyniesie \(\displaystyle{a\approx 4,2\,\mathrm{\frac{m}{s^2}}}\)  siła naciągu \(N=1,16\,\mathrm{N}\).