Analiza sytuacji

Na rysunku przedstawiono staczające się z równi ciało, którym może być zarówno kula, jak i obręcz.

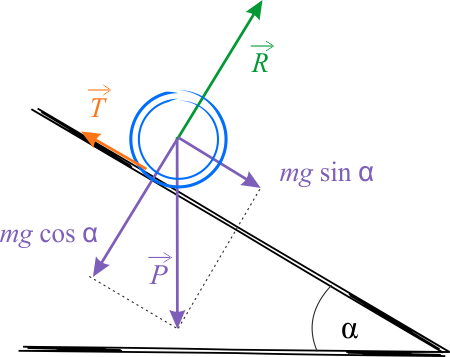
Na staczające się ciało działa siła ciężkości $mg$, gdzie $m$ jest jego masą, a $g$ wektorem przyspieszenia ziemskiego. Siła ta jest sumą wszystkich sił działających na poszczególne punkty ciała i można ją zastąpić jedną siłą, działającą na środek masy. Siłę tę wygodnie jest rozłożyć na dwie składowe: składową równą, co do wartości $mg\, \cos\alpha$, prostopadłą do powierzchni równi, czyli siłę nacisku i składową styczną do powierzchni równi $mg\, \sin\alpha$. Siła nacisku jest w całości równoważona siłą reakcji równi, a składowa styczna częściowo siłą tarcia o wartości $T$ i przeciwnym do niej zwrocie. Wypadkowa wszystkich sił działających na ciało powoduje, zgodnie z drugą zasadą dynamiki, ruch ciała z przyspieszeniem $a$ takim, że


Powyższe równanie opisuje ruch postępowy środka masy ciała. Z kolei ruch obrotowy wokół osi przechodzącej przez środek masy jest uwarunkowany wypadkowym momentem sił działających na ciało. Zgodnie z definicją moment siły wynosi


W naszym przypadku siła ciężkości (bądź tworzące ją składowe) jest przyłożona w środku masy ciała, dlatego jej moment jest równy zeru. Z kolei moment siły reakcji równy jest zero, gdyż co prawda punkt przyłożenia siły reakcji jest na obwodzie ciała, ale działa ona wzdłuż ramienia, czyli kąt $\varphi$ we wzorze na moment $M$ jest równy zeru. Jedyną siłą dającą niezerowy moment jest siła tarcia. Wartość momentu siły $T$ wynosi $RT$, gdzie $R$ jest promieniem staczającego się ciała. Moment siły $T$ powoduje ruch obrotowy z przyspieszeniem kątowym $\varepsilon$. W naszym przypadku


gdzie $I$ jest momentem bezwładności ciała, tj. kuli lub obręczy. Moment bezwładności kuli dany jest w zadaniu, a moment bezwładności obręczy o masie $m_o$ i promieniu $R_o$ wynosi $m_oR_o^2$ (zakładając, że obręcz jest cienka i wszystkie punkty masy obręczy znajdują się w tej samej odległości od osi obrotu).

Rozwiązanie

Przepiszmy teraz równania ruchu postępowego i obrotowego obu ciał, zakładając, że mogą one mieć dowolne masy (wielkości dotyczące kuli oznaczmy znakiem $k$ a obręczy - $o$). Zakładamy także, że ciała staczają się bez poślizgu, a stąd związek między przyspieszeniem kątowym $\varepsilon$ a przyspieszeniem środka masy $a$ ma postać $\displaystyle{\varepsilon=\frac{a}{R} }$.

Kula

Obręcz    
Rozwiązując powyższe układy równań  Jak?  Z drugiego równania mamy $\displaystyle{T_k=\frac{2}{5}m_ka_k }$ i podstawiając otrzymaną wartość do równania pierwszego otrzymujemy $$\displaystyle{m_kg\sin\alpha-\frac{2}{5}m_ka_k=m_ka_k}$$ $$\displaystyle{g\sin\alpha=\frac{7}{5}a_k}$$ Dla obręczy postępujemy analogicznie.  , znajdujemy odpowiednio przyspieszenie środka masy kuli i obręczy.


Zauważmy po pierwsze, że otrzymane przyspieszenia nie zależą od masy i promieni staczających się ciał. Po drugie, przyspieszenie kuli jest większe, więc aby oba ciała przebyły tą samą odległość w tym samym czasie $t$, obręczy należy nadać pewną prędkość początkową $v_0$.

Niech droga przebyta przez ciała w czasie $t$ wynosi $S$. Możemy napisać:


Porównując powyższe wyrażenia na drogę otrzymujemy równanie

 Przekształcenia   $$\displaystyle{v_0=\frac{a_kt}{2}-\frac{a_ot}{2}}$$ $$\displaystyle{v_0=\frac{t}{2}(a_k-a_o)}$$ $$\displaystyle{v_0=\frac{t}{2}\left (\frac{5}{7}g\sin\alpha -\frac{1}{2}g\sin\alpha\right )}$$ $$\displaystyle{v_0=\frac{1}{2}tg\,\sin\alpha\left (\frac{5}{7}-\frac{1}{2}\right )}$$